DigitalServo

Blog

About

Library

January 8, 2023, JST

擬似微分器の設計について

H. Kurumatani

keywords:

制御工学

擬似微分器について

　離散時間制御系では完全微分を行うことができないため，フィルタや観測器を用いた不完全微分による微分値推定が行われます。例えば，純粋な微分特性を表す ss は非プロパであり，実装することができません。そのため，低域通過フィルタと組み合わせてプロパなシステムとして実装する手法があります。この方法で得られるフィルタの一例を以下に示します。ただし，gg は低域通過フィルタの遮断周波数 [rad/s][\rm rad/s] を表すものとします。
x˙^=gs+gsx≡D1(s)x\begin{align} \hat{\dot{x}} &= \frac{g}{s+g}s x \\ &\equiv D_{1}(s)x \end{align}
フィルタ D1D_1 は 0∼g [rad/s]0 \sim g\ [{\rm rad/s}] の周波数帯域で微分器 ss と近しい特性を示します。このような不完全微分を行うシステムを擬似微分器と呼びます。

擬似微分器の特性

　上記の擬似微分器 D1D_{1} は，一定速度で変動する状態量に対して誤差なく微分値を推定可能であることが最終値の定理より確認できます。時刻 tt，定数 C1C_1 を用いて状態 xx が x(t)=C1t (x(0)=0)x(t)=C_1t\ (x(0)=0) となるように時間遷移する場合，以下の式が成立します。
x=∫0∞C1te−stdt=s−2C1e(s)≡sx−gs+gsxlim⁡s→0se(s)=lim⁡s→0ss2s+gx=lim⁡s→0sC1s+gx=0\begin{align} x&= \int^{\infty}_{0} C_1t e^{-st}dt \\ &= s^{-2}C_1\\ e(s) & \equiv sx -\frac{g}{s+g}s x \\ \lim_{\rm s\rightarrow 0}se(s) &= \lim_{\rm s\rightarrow 0} s\frac{s^2}{s+g} x\\ &=\lim_{\rm s\rightarrow 0} \frac{sC_1}{s+g} x\\ &=0 \end{align}
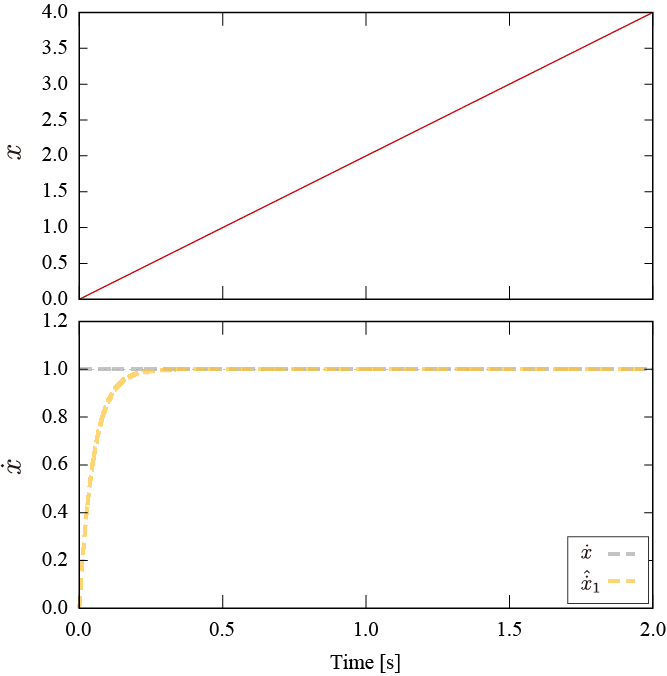
以下に C1=1, g=10C_1=1,\ g=10 とした際の状態 x, x˙x,\ \dot{x} および擬似微分機 D1D_1 による推定微分値 x˙^1\hat{\dot{x}}_1 を示します。定常状態において推定微分値は真値に一致していることが確認できます。
image is here
しかしながら，状態 xx が一定加速度で変動する場合に，擬似微分器 D1D_1 は推定誤差を 00 に収束することができません。時刻 tt，定数 C2C_2 を用いて状態 xx が x(t)=C2t2 (x(0)=x˙(0)=0)x(t)=C_2t^2\ (x(0)=\dot{x}(0)=0) となるように時間遷移する場合，以下の式が成立します。
x=∫0∞C2t2e−stdt=s−3C1lim⁡s→0se(s)=lim⁡s→0ss2s+gx=lim⁡s→0C2s+gx≠0\begin{align} x&= \int^{\infty}_{0} C_2t^2 e^{-st}dt \\ &= s^{-3}C_1\\ \lim_{\rm s\rightarrow 0}se(s) &= \lim_{\rm s\rightarrow 0} s\frac{s^2}{s+g} x\\ &=\lim_{\rm s\rightarrow 0} \frac{C_2}{s+g} x\\ &\neq 0 \end{align}
以上より，微分値推定において定常偏差が残ることが確認できます。この原因は状態 xx の生成過程を考慮しないことに起因します。次節より，観測器の設計理論に基づいて擬似微分器の設計について考えます。

微分状態量に対する観測器の設計

　状態の生成過程を考慮し，状態量の微分値に対して観測器を設計します。擬似微分器 D1D_1 は一定速度で変動する状態の微分値は誤差なく推定可能でしたが，一定加速度で変動する状態に対しては推定微分値に定常偏差が残りました。すなわち，D1D_1は速度変動のない状態量 (x¨=0\ddot{x}=0となる状態量 xx) に対して正しく推定を行う観測器と見ることができます。これを基に観測器のモデルを作成する場合，以下のように記述することができます。
ddt[xx˙]=[0100][xx˙]+vy=[10][xx˙]+w \begin{align} \frac{d}{dt}\begin{bmatrix} x \\ \dot{x} \end{bmatrix} &= \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \end{bmatrix} + v\\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \end{bmatrix} + w\ \end{align}
ただし，v, wv,\ w はプロセス雑音および観測雑音を表します。プロセス雑音は遷移プロセスに生じる誤差を表現するものであり，モデル化誤差の影響はプロセス雑音に含まれます。すなわち，状態の考慮されていない高階微分項はこの雑音として扱われます。このモデルを使用して最小次元オブザーバを設計すると，以下の推定式が導出されます。ただし，LL はオブザーバゲインを表します。
x˙^=Ls+Lsx\begin{align} \hat{\dot{x}} &= \frac{L}{s+L}s x \\ \end{align}
したがって，上記の観測器は擬似微分器 D1D_1と等価な推定特性を有します。観測器はモデル誤差による状態遷移に対して推定誤差の収束を保証しないため，一定加速度で変動する状態に対して微分値を推定した場合に定常偏差を取り除くことができません。そこで，状態の加速度が一定と仮定したモデルを用意して観測器を設計します。
ddt[xx˙x¨]=[010001000][xx˙x¨]+vy=[100][xx˙x¨]+w \begin{align} \frac{d}{dt}\begin{bmatrix} x \\ \dot{x} \\ \ddot{x} \end{bmatrix} &= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \\ \ddot{x} \end{bmatrix} + v\\ y &= \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \\ \ddot{x} \end{bmatrix} + w\ \end{align}
このモデルを使用して最小次元オブザーバを設計すると，以下の推定式が導出されます。ただし，l1,l2l_1, l_2 はオブザーバゲインを表します。
[x˙x¨]=1s2+l1s+l2[l1s2+l2sl2s]x\begin{align} \begin{bmatrix} \dot{x} \\ \ddot{x} \end{bmatrix} &= \frac{1}{s^2+l_1s+l_2}\begin{bmatrix} l_1s^2 + l_2s \\ l_2s \end{bmatrix}x \end{align}
したがって，微分値の推定は次のように行われます。
x˙=l1s+l2s2+l1s+l2sx≡D2(s)x\begin{align} \dot{x} &= \frac{l_1s+l_2}{s^2+l_1s+l_2}sx\\ &\equiv D_2(s)x \end{align}
ここで，D2D_2 が D1D_1 に近しい周波数特性を有するように，以下のようにオブザーバゲインを決定します (決定方法について)。
[l1l2]=[gg2/4]\begin{align} \begin{bmatrix} l_1 & l_2 \end{bmatrix} &= \begin{bmatrix} g & g^2/4 \end{bmatrix} \end{align}
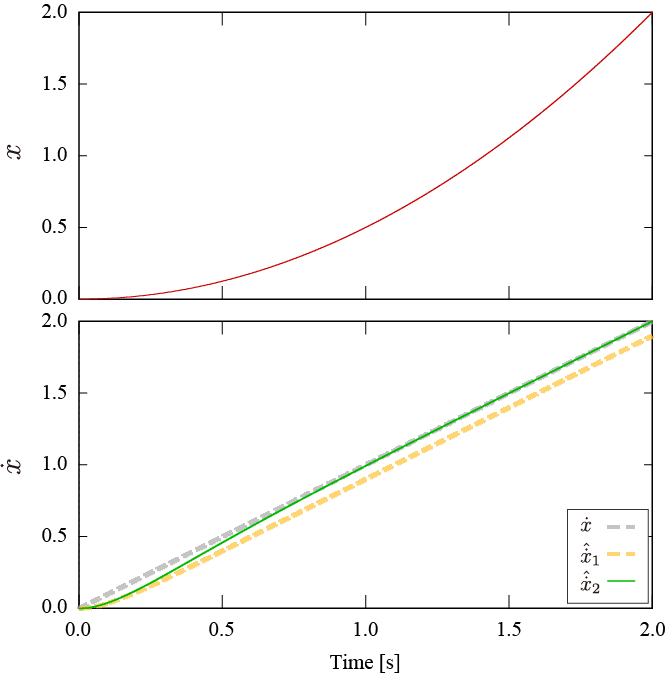
このとき，C2=0.5, g=10C_2=0.5,\ g=10 とした際の状態 x, x˙x,\ \dot{x} および D1, D2D_1,\ D_2による推定微分値 x˙^1, x˙^2\hat{\dot{x}}_1,\ \hat{\dot{x}}_2 を示します。
image is here
状態の一定速度変動を仮定した擬似微分器 D1D_1 では推定値に定常偏差が残るのに対し，状態の一定加速度変動を仮定した擬似微分器 D2D_2 では推定値が真値に漸近します。したがって，周波数特性の設計だけでなく，状態の生成過程を擬似微分器設計に導入することで推定誤差が抑圧可能であることが確認できました。モーションコントロールで使用される外乱オブザーバでは外乱のダイナミクスを考慮した拡張状態空間表現を用いた設計がされており，外乱推定における定常偏差の除去がなされています。また，センサレスベクトル制御で使用される磁束オブザーバでは，回転のダイナミクスをモデルに導入することで高い周波数を有する周期信号に対して位相遅れの少ない磁束推定を実現しています。

システムの入力および動特性を考慮した設計

　制御入力が利用可能である場合には，状態量の生成過程についてモデルを用意するのではなく，制御入力とシステムの動特性から状態量の生成過程を予測することができます。制御入力が利用可能な場合に，観測器の推定誤差抑圧機構は二自由度制御系構造を有しており，制御入力項は推定のフィードフォワードとして機能します。システムの動的モデルが正確である場合に，入力およびモデルから予測される状態量の遷移は状態量の生成過程と一致します。

以下に示すSISO系について考えます。ただし，uu を入力とし，外乱および雑音は存在しないものとします。
ddt[xx˙]=[0100][xx˙]+[01]uy=[10][xx˙]\begin{align} \frac{d}{dt}\begin{bmatrix} x \\ \dot{x} \end{bmatrix} &= \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \end{bmatrix} \end{align}
このモデルを使用して最小次元オブザーバを設計することで，以下の推定式を得ます。ただし，LL はオブザーバゲインを表します。
x˙^=1s+Lu+Ls+Lsx\begin{align} \hat{\dot{x}} &= \frac{1}{s+L}u + \frac{L}{s+L}s x \\ \end{align}
上記の観測器を擬似微分器 D3D_3 とします。ここで，入力として以下を与えるものとします。
u=x¨ref+Kp(xref−x)+Kd(x˙ref−x˙)xref={0.0(t<0.5)0.5(1.0−cos⁡(6πt))(0.5≤t<0.5+1/6)1.0(t≤0.5+1/6)Kp=10000.0Kd=200.0\begin{align} u &= \ddot{x}^{\rm ref} + K_{\rm p} (x^{\rm ref} - x) + K_{\rm d}(\dot{x}^{\rm ref} - \dot{x}) \\ x^{\rm ref} &= \left\{ \begin{array}{ll} 0.0 & (t<0.5) \\ 0.5\left( 1.0 - \cos(6\pi t)\right) & (0.5 \le t < 0.5 + 1/6)\\ 1.0 & (t\le 0.5 + 1/6) \end{array} \right.\\ K_{\rm p} &= 10000.0\\ K_{\rm d} &= 200.0 \\ \end{align}
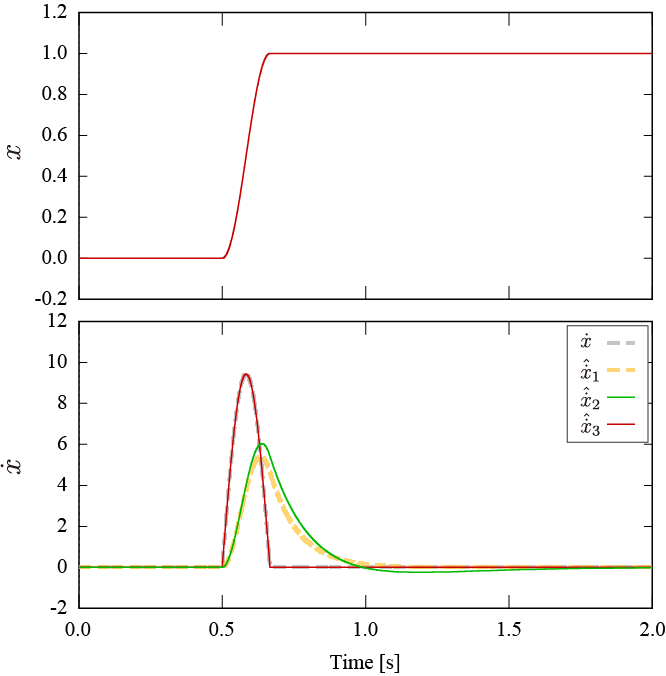
このとき，状態 x,x˙x, \dot{x} および擬似微分機 D1, D2, D3D_1,\ D_2,\ D_3 による推定値 x˙^1, x˙^2, x˙^3\hat{\dot{x}}_1,\ \hat{\dot{x}}_2,\ \hat{\dot{x}}_3 は以下のようになりました。
image is here
入力を使用しない擬似微分器 D1, D2D_1,\ D_2 では推定値の振幅減衰および位相遅れが表れました。D2D_2 による推定では推定式に存在する零点の影響により推定立ち上がり時の振幅・位相特性の改善が見られますが，立ち下がり時にアンダーシュートが確認できます。一方で，入力による予測式を導入した擬似微分器 D3D_3 では，振幅減衰・位相遅れのない推定が達成されています。状態が確定的な外因性入力の影響を受ける場合には，そのモデルを導入することで推定誤差を低減することができます。

© DigitalServo