外乱オブザーバはシステムに作用する外乱を推定するオブザーバである。
本オブザーバによる推定外乱値を用いて制御系を構築することにより外乱抑圧特性の設計自由度が与えられ、簡潔な二自由度制御系の設計が可能となる。
以下では外乱オブザーバの設計方法、外乱抑圧特性の設計方法、および制御系の構造的特徴について確認する。
外乱オブザーバは外乱をシステムの状態に含めた拡張状態空間表現に対して最小次元オブザーバを構成することで設計される。
以下に示す状態空間表現について考える。
x ˙ = A x + D d d + B u d ˙ = A d d y = C x \begin{align}
\dot{\bm{x}}&=\bm{A}\bm{x}+\bm{D}_{\rm d}\bm{d}+\bm{B}\bm{u}\\
\dot{\bm{d}}&=\bm{A}_{\rm d}\bm{d}\\
\bm{y}&=\bm{C}\bm{x}
\end{align} x ˙ d ˙ y = A x + D d d + B u = A d d = C x ただし、
A , B , C , D \bm{A}, \bm{B}, \bm{C}, \bm{D} A , B , C , D はそれぞれシステム行列、入力行列、観測行列、および外乱行列を表す。また、
x , y , u , d \bm{x}, \bm{y}, \bm{u}, \bm{d} x , y , u , d は状態、出力、入力、および外乱を表す。下添字
d _{\rm d} d は外乱のダイナミクスに関するシステムであることを示す。ここでは入力、状態、および外乱に相関関係が存在しないものとする。ここで、外乱をシステムの状態と見做して次の拡張状態空間表現を得る。
z ˙ = [ A d 0 D d A ] z + [ 0 B ] u y = [ 0 C ] z \begin{align}
\dot{\bm{z}}&=
\begin{bmatrix}
\bm{A}_{\rm d} & \bm{0}\\
\bm{D}_{\rm d} & \bm{A}
\end{bmatrix}\bm{z}+
\begin{bmatrix}
\bm{0} \\ \bm{B}
\end{bmatrix}\bm{u}\\
\bm{y}&=\begin{bmatrix}
\bm{0} & \bm{C}
\end{bmatrix}\bm{z}
\end{align} z ˙ y = [ A d D d 0 A ] z + [ 0 B ] u = [ 0 C ] z ただし、このシステムの状態
z \bm{z} z は次のように定義される。
z ≡ [ d x ] T \begin{align}
\bm{z}&\equiv
\begin{bmatrix}
\bm{d} & \bm{x}
\end{bmatrix}^{\mathrm T}
\end{align} z ≡ [ d x ] T 続いて、この拡張状態空間表現に対して
最小次元オブザーバ を構成することを検討する。状態
z \bm{z} z を測定可能な状態
y \bm{y} y と 測定不可の状態
ξ \bm{\xi} ξ に分離して並び替え、拡張状態空間表現を次のように再構成する。
z ˙ ′ = [ A z 11 A z 12 A z 21 A z 22 ] z ′ + [ B z 1 B z 2 ] u z z ′ = [ ξ y ] T \begin{align}
\dot{\bm{z}}'&=
\begin{bmatrix}
\bm{A}_{z11} &\bm{A}_{z12}\\
\bm{A}_{z21} &\bm{A}_{z22}
\end{bmatrix}
\bm{z}'+
\begin{bmatrix}
\bm{B}_{z1}\\\bm{B}_{z2}
\end{bmatrix}\bm{u}_{z}\\
\bm{z}'&=
\begin{bmatrix}
\bm{\xi} & \bm{y}
\end{bmatrix} ^{\mathrm T}
\end{align} z ˙ ′ z ′ = [ A z 11 A z 21 A z 12 A z 22 ] z ′ + [ B z 1 B z 2 ] u z = [ ξ y ] T このとき、不可測定量
ξ \bm{\xi} ξ に対する観測器は次のように構成される。
ξ ^ = ( s I − T ξ ) − 1 { T u u + ( s L + T y ) y } \begin{align}
\hat{\bm{\xi}} =(s\bm{I}-\bm{T}_{\xi})^{-1} \left\{ \bm{T}_{u} \bm{u} + (s\bm{L} + \bm{T}_{y})\bm{y} \right\}
\end{align} ξ ^ = ( s I − T ξ ) − 1 { T u u + ( s L + T y ) y } ただし、
T ξ , T u , T y \bm{T}_{\xi}, \bm{T}_{u}, \bm{T}_{y} T ξ , T u , T y は係数行列であり、以下のように定義される。
T ξ ≡ A z 11 − L A z 21 T u ≡ B z 1 − L B z 2 T y ≡ A z 12 − L A z 22 \begin{align}
\bm{T}_{\xi} &\equiv \bm{A}_{{\rm z}11}-\bm{L}\bm{A}_{{\rm z} 21}\\
\bm{T}_{u} &\equiv \bm{B}_{{\rm z}1}-\bm{L}\bm{B}_{{\rm z}2}\\
\bm{T}_{y} &\equiv \bm{A}_{{\rm z}12}-\bm{L}\bm{A}_{{\rm z}22}
\end{align} T ξ T u T y ≡ A z 11 − L A z 21 ≡ B z 1 − L B z 2 ≡ A z 12 − L A z 22 簡単のため不可測定量
ξ = d \bm{\xi}=\bm{d} ξ = d かつ 可測定量
y = x \bm{y}=\bm{x} y = x の場合について考えると、外乱推定器は次のように構成される。
d ^ = ( s I − A d + L D d ) − 1 L { − B u + ( s I − A ) y } \begin{align}
\hat{\bm{d}} &= (s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1}\bm{L}\{-\bm{B}\bm{u}+(s\bm{I}-\bm{A})\bm{y}\}
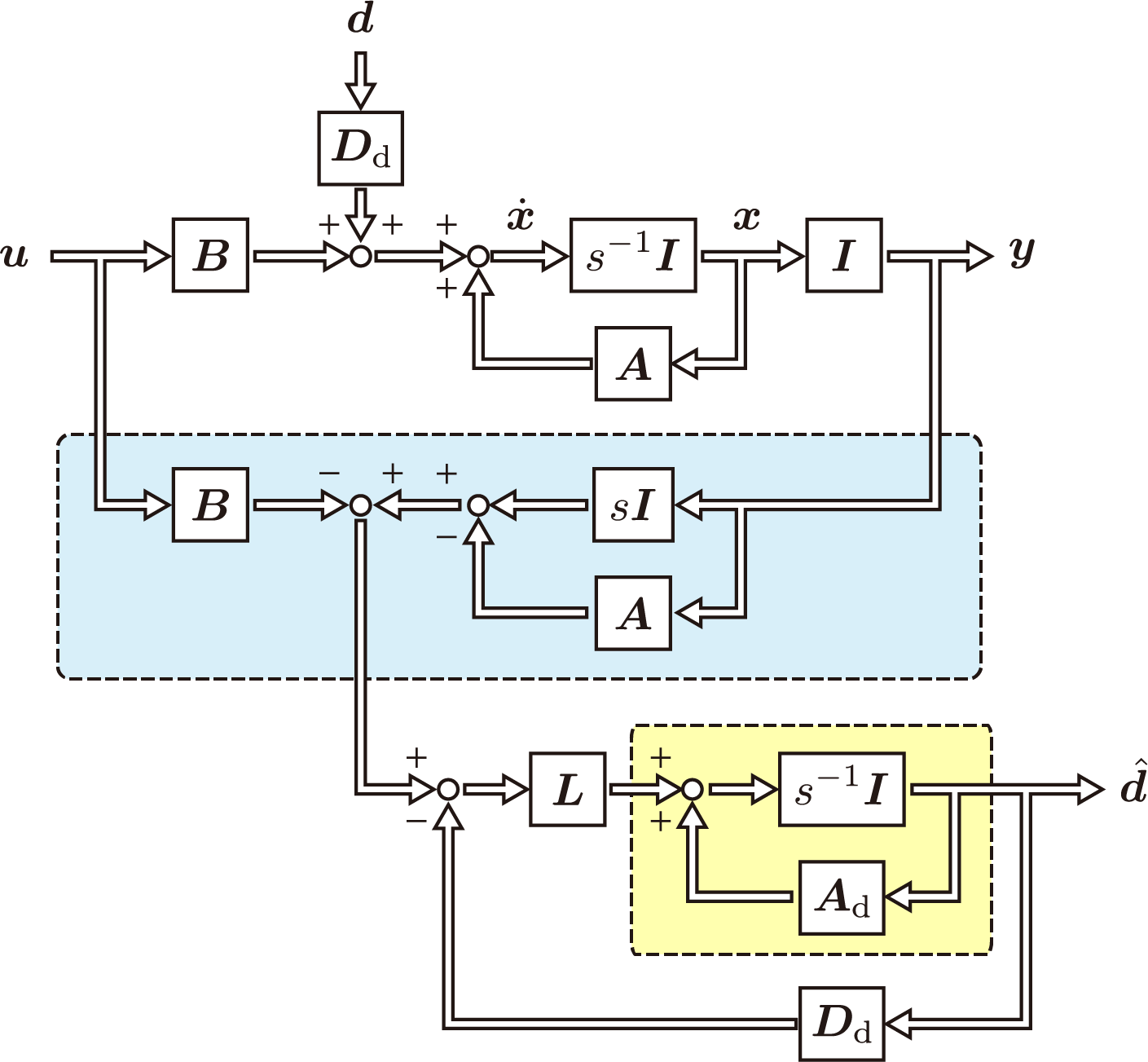
\end{align} d ^ = ( s I − A d + L D d ) − 1 L { − B u + ( s I − A ) y } この条件においてシステムのブロック線図は次のように表現される。
ここで、青枠部は外乱の逆算を行う機構、その下部はフィルタリングする機構と見ることができる。フィルタリング部における黄枠部は外乱生成のダイナミクスを示しており、
内部モデル原理 の観点から外乱推定誤差の収束について重要な役割を果たす。
外乱オブザーバによって推定される推定外乱値は次のように記述される。
d ^ = ( s I − A d + L D d ) − 1 L D d d \begin{align}
\hat{\bm{d}} &= (s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1}\bm{L}\bm{D}_{\rm d}\bm{d}\\
\end{align} d ^ = ( s I − A d + L D d ) − 1 L D d d このとき、推定誤差は次のように計算される。
d − d ^ = { I − ( s I − A d + L D d ) − 1 L D d } d = ( s I − A d + L D d ) − 1 ( s I − A d ) d = − ( s I − A d + L D d ) − 1 d 0 \begin{align}
\bm{d} - \hat{\bm{d}} &=\left\{\bm{I} -(s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1}\bm{L}\bm{D}_{\rm d} \right\} \bm{d} \\
&= (s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1}\left( s\bm{I} -\bm{A}_{\rm d} \right) \bm{d} \\
&= -(s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1} \bm{d}_{0}
\end{align} d − d ^ = { I − ( s I − A d + L D d ) − 1 L D d } d = ( s I − A d + L D d ) − 1 ( s I − A d ) d = − ( s I − A d + L D d ) − 1 d 0 ただし、
d 0 \bm{d}_{0} d 0 は外乱
d \bm{d} d の初期値を表す。したがって、推定器が安定であれば推定誤差は
0 \bm{0} 0 に収束する。
外乱オブザーバによる外乱推定機構を確認すると、次のような推定構造を見つけることができる。
d ^ = F U F ≡ ( s I − A d + L D d ) − 1 L U ≡ { − B u + ( s I − A ) y } \begin{align}
\hat{\bm{d}} &= \bm{F} \bm{U}\\
\bm{F} &\equiv (s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1}\bm{L} \\
\bm{U} &\equiv \{-\bm{B}\bm{u}+(s\bm{I}-\bm{A})\bm{y}\}
\end{align} d ^ F U = F U ≡ ( s I − A d + L D d ) − 1 L ≡ { − B u + ( s I − A ) y } ここで、
U \bm{U} U は入力
u \bm{u} u および可測定量
y \bm{y} y から予測可能な信号、
F \bm{F} F は 信号
U \bm{U} U に対するフィルタと見ることができる。信号
U \bm{U} U の予測には外乱を含まないシステムの情報のみが必要であり、その予測機構は外乱のダイナミクスに関わらず不変となる。一方で、外乱の情報はフィルタ
F \bm{F} F に集約される。すなわち、外乱のダイナミクス
A d \bm{A}_{\rm d} A d を用いてフィルタ
F \bm{F} F を直接設計することで外乱オブザーバを構築することができる。
一定値外乱の推定を目的として、外乱のダイナミクスを次のように仮定して設計された外乱オブザーバを0次外乱オブザーバと呼ぶ。これは
A d = 0 \bm{A}_{\rm d}=\bm{0} A d = 0 を意味する。
d ˙ = 0 \begin{align}
\dot{\bm{d}} = \bm{0}
\end{align} d ˙ = 0 このとき、外乱推定フィルタは次のように表される。
F = ( s I + L D d ) − 1 L \begin{align}
\bm{F}=(s\bm{I}+\bm{L}\bm{D}_{{\rm d}})^{-1}\bm{L}
\end{align} F = ( s I + L D d ) − 1 L 一定値外乱に加え、ランプ外乱、パラボラ外乱等の推定を目的として、外乱のダイナミクスを次のように仮定して設計された外乱オブザーバを n 次外乱オブザーバと呼ぶ。
d d t [ d d ( 1 ) ⋮ d ( n − 1 ) d ( n ) ] = [ 0 I ⋯ ⋯ 0 0 0 I 0 ⋮ ⋱ ⋱ ⋮ 0 ⋯ ⋯ 0 I 0 ⋯ ⋯ ⋯ 0 ] [ d d ( 1 ) ⋮ d ( n − 1 ) d ( n ) ] \begin{align}
\frac{d}{dt}
\begin{bmatrix}
\bm{d} \\
\bm{d}^{({\rm 1})} \\
\vdots \\
\bm{d}^{({\rm n-1})} \\
\bm{d}^{({\rm n})}
\end{bmatrix}
=
\begin{bmatrix}
\bm{0} & \bm{I} & \cdots & \cdots & \bm{0} \\
\bm{0} & \bm{0} & \bm{I} & & \bm{0} \\
\vdots & & \ddots & \ddots & \vdots \\
\bm{0} & \cdots & \cdots & \bm{0} & \bm{I} \\
\bm{0} & \cdots & \cdots & \cdots & \bm{0}
\end{bmatrix}
\begin{bmatrix}
\bm{d} \\
\bm{d}^{({\rm 1})} \\
\vdots \\
\bm{d}^{({\rm n-1})} \\
\bm{d}^{({\rm n})}
\end{bmatrix}
\end{align} d t d d d ( 1 ) ⋮ d ( n − 1 ) d ( n ) = 0 0 ⋮ 0 0 I 0 ⋯ ⋯ ⋯ I ⋱ ⋯ ⋯ ⋯ ⋱ 0 ⋯ 0 0 ⋮ I 0 d d ( 1 ) ⋮ d ( n − 1 ) d ( n ) 推定外乱をフィードバックすることで外乱を相殺し、システムに作用する外乱の影響を抑圧することができる。
以下の状態空間表現によって記述されるシステムを考える。
x ˙ = A x + D d d + B u d ˙ = A d d y = x \begin{align}
\dot{\bm{x}}&=\bm{A}\bm{x}+\bm{D}_{\rm d}\bm{d}+\bm{B}\bm{u}\\
\dot{\bm{d}}&=\bm{A}_{\rm d}\bm{d}\\
\bm{y}&=\bm{x}
\end{align} x ˙ d ˙ y = A x + D d d + B u = A d d = x ただし、
A , B , C , D \bm{A}, \bm{B}, \bm{C}, \bm{D} A , B , C , D はそれぞれシステム行列、入力行列、観測行列、および外乱行列を表す。また、
x , y , u , d \bm{x}, \bm{y}, \bm{u}, \bm{d} x , y , u , d は状態、出力、入力、および外乱を表す。下添字
d _{\rm d} d は外乱のダイナミクスに関するシステムであることを示す。ここで、制御入力
u \bm{u} u を次のように設計する。
u = u r e f − K d ^ d ^ = F { − B u + ( s I − A ) y } \begin{align}
\bm{u} &= \bm{u}^{\rm ref} - \bm{K}\hat{\bm{d}}\\
\hat{\bm{d}} &= \bm{F} \{-\bm{B}\bm{u}+(s\bm{I}-\bm{A})\bm{y}\}
\end{align} u d ^ = u ref − K d ^ = F { − B u + ( s I − A ) y } ここで、
K \bm{K} K はフィードバックゲイン、
F \bm{F} F は任意の安定なフィルタを表し、
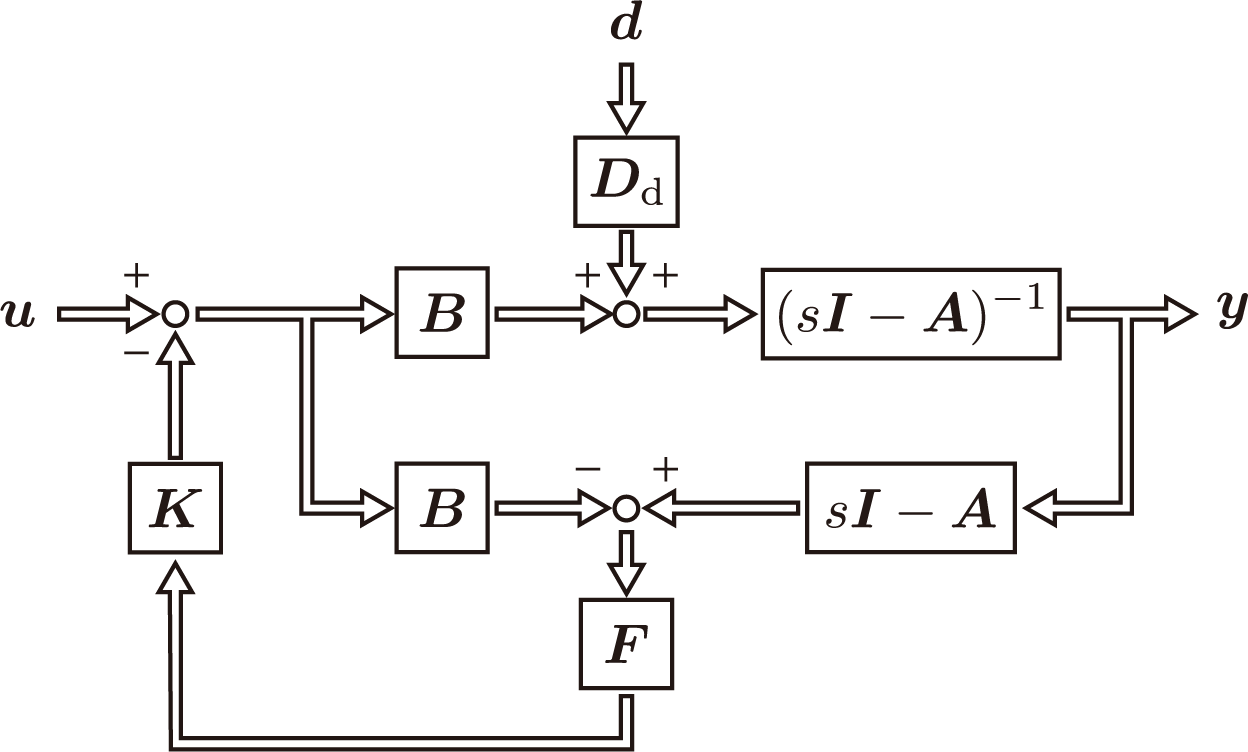
u r e f \bm{u}^{\rm ref} u ref は制御系に対する参照入力を表す。参照入力の設計によって指令値追従特性の整形が可能となる。この制御系のブロック線図は次のように表現される。
この制御則を適用することにより、状態
u \bm{u} u に関して次の代数方程式が成立する。
u = u r e f − K F { − B u + ( s I − A ) y } = u r e f − K F D d d \begin{align}
\bm{u} &= \bm{u}^{\rm ref} - \bm{K}\bm{F} \{-\bm{B}\bm{u}+(s\bm{I}-\bm{A})\bm{y}\}\\
&= \bm{u}^{\rm ref} - \bm{K}\bm{F}\bm{D}_{\rm d}\bm{d}
\end{align} u = u ref − K F { − B u + ( s I − A ) y } = u ref − K F D d d したがって、このフィードバック系のダイナミクスは次のように表現される。
x ˙ = A x + D d d + B ( u r e f − K F D d d ) = A x + B u r e f + ( D d − B K F D d ) d \begin{align}
\dot{\bm{x}}&=\bm{A}\bm{x}+\bm{D}_{\rm d}\bm{d}+\bm{B}(\bm{u}^{\rm ref} - \bm{K}\bm{F}\bm{D}_{\rm d}\bm{d})\\
&=\bm{A}\bm{x} +\bm{B}\bm{u}^{\rm ref} + (\bm{D}_{\rm d}- \bm{B}\bm{K}\bm{F}\bm{D}_{\rm d})\bm{d}
\end{align} x ˙ = A x + D d d + B ( u ref − K F D d d ) = A x + B u ref + ( D d − B K F D d ) d 上式より、推定外乱フィードバックによって指令値追従特性の設計自由度を確保しつつ外乱抑圧を達成することが確認できる。また、
B K = D d \bm{B}\bm{K} = \bm{D}_{\rm d} B K = D d となるようにフィードバックゲイン
K \bm{K} K を設計することができれば、制御系のダイナミクスは次のように表現される。
x ˙ = A x + B u r e f + D d ( I − F D d ) d \begin{align}
\dot{\bm{x}} &= \bm{A}\bm{x} +\bm{B}\bm{u}^{\rm ref} + \bm{D}_{\rm d}(\bm{I} - \bm{F}\bm{D}_{\rm d})\bm{d}
\end{align} x ˙ = A x + B u ref + D d ( I − F D d ) d 特に、外乱推定フィルタ
F \bm{F} F について外乱のダイナミクスを考慮した設計を行うことにより、外乱の完全な抑圧が可能となる。
F = ( s I − A d + L D d ) − 1 L → D d ( I − F D d ) d = D d ( s I − A d + L D d ) − 1 d 0 \begin{align}
\bm{F} &= (s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1}\bm{L} \\
\rightarrow \bm{D}_{\rm d}(\bm{I} - \bm{F}\bm{D}_{\rm d})\bm{d} &= \bm{D}_{\rm d}(s\bm{I}-\bm{A}_{{\rm d}}+\bm{L}\bm{D}_{{\rm d}})^{-1}\bm{d}_{0}
\end{align} F → D d ( I − F D d ) d = ( s I − A d + L D d ) − 1 L = D d ( s I − A d + L D d ) − 1 d 0 ただし、
d 0 \bm{d}_{0} d 0 は外乱
d \bm{d} d の初期値を表す。以上より、外乱オブザーバを用いた外乱抑圧機構は外乱抑圧特性に関する独立した設計自由度を与え、指令値追従制御器と合わせて二自由度制御系を構築することができる。
外乱オブザーバは状態空間表現から設計される最小次元オブザーバであり、現代制御の枠組みから導出されたものであるが、古典制御の枠組みでも設計することができる。古典制御ではシステムの周波数特性を考慮しやすく、外乱オブザーバの設計を周波数領域で検討することが可能となる。
ここではプラントを
P \bm{P} P , 入出力および外乱を
u , y , d \bm{u}, \bm{y}, \bm{d} u , y , d として、制御対象が以下のように表現される場合について考える。
y = P ( u + d ) \begin{align}
\bm{y} = \bm{P}(\bm{u} + \bm{d})
\end{align} y = P ( u + d ) このシステムに対して、プラントのノミナルモデルおよび外乱推定フィルタを
P n , F \bm{P}_{\rm n}, \bm{F} P n , F とし、外乱オブザーバは次のように設計される。ただし、添字
^ \ \hat{} ^ は推定値を表す。
d ^ = F ( − u + P n − 1 y ) \begin{align}
\hat{\bm{d}} = \bm{F}(-\bm{u} + \bm{P}^{-1}_{\rm n}\bm{y})
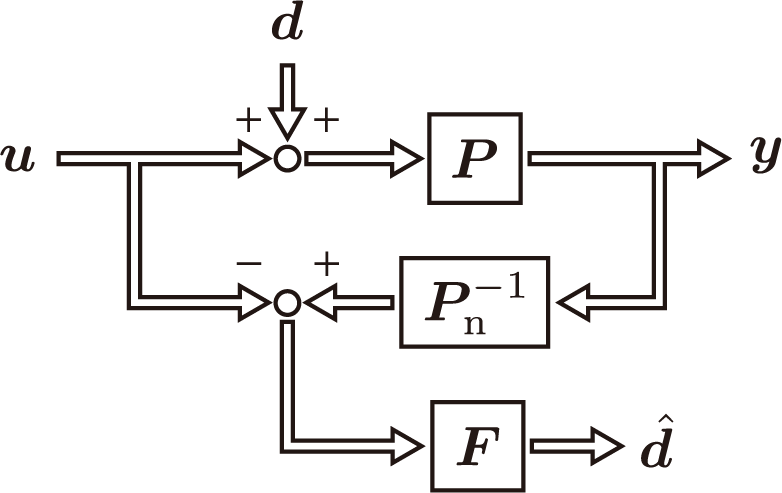
\end{align} d ^ = F ( − u + P n − 1 y ) このとき、制御系のブロック線図は次のように表現される。
ここで、
F \bm{F} F は自身と
F P n − 1 \bm{F}\bm{P}^{-1}_{\rm n} F P n − 1 が安定かつプロパとなるように設計する。プラントモデルの逆行列
P n − 1 \bm{P}^{-1}_{\rm n} P n − 1 は一般に非プロパであり、またプラントが不安定零点を有する場合に
P n \bm{P}_{\rm n} P n は不安定極を持つ。そのような場合には
F \bm{F} F に厳密にプロパなフィルタや不安定極を相殺するオールパスフィルタを導入することで
F P n − 1 \bm{F}\bm{P}^{-1}_{\rm n} F P n − 1 を安定かつプロパとすることができる。ここで、次のフィードバック制御器を設計することを考える。
u = u r e f − d ^ \begin{align}
\bm{u} &= \bm{u}^{\rm ref} - \hat{\bm{d}}
\end{align} u = u ref − d ^ ただし、
u r e f \bm{u}^{\rm ref} u ref は制御系に対する参照入力を表す。ここで、
u \bm{u} u に関して次の代数方程式が成立する。
u = u r e f − d ^ = u r e f + F ( u − P n − 1 y ) = u r e f + F { u − P n − 1 P ( u + d ) } ∴ u = { ( I − F ) + F P n − 1 P ) } − 1 ( u r e f − F P n − 1 P d ) \begin{align}
\bm{u} &= \bm{u}^{\rm ref} - \hat{\bm{d}} \\
&= \bm{u}^{\rm ref} + \bm{F}(\bm{u} - \bm{P}^{-1}_{\rm n}\bm{y}) \\
&= \bm{u}^{\rm ref} + \bm{F}\{\bm{u} - \bm{P}^{-1}_{\rm n} \bm{P}(\bm{u} + \bm{d})\} \\
\therefore \bm{u} &= \{(\bm{I} - \bm{F}) + \bm{F}\bm{P}^{-1}_{\rm n} \bm{P})\}^{-1} (\bm{u}^{\rm ref} - \bm{F}\bm{P}^{-1}_{\rm n}\bm{P}\bm{d})
\end{align} u ∴ u = u ref − d ^ = u ref + F ( u − P n − 1 y ) = u ref + F { u − P n − 1 P ( u + d )} = {( I − F ) + F P n − 1 P ) } − 1 ( u ref − F P n − 1 P d ) したがって、出力
y \bm{y} y は次のように記述される。
y = P { ( I − F ) + F P n − 1 P ) } − 1 { u r e f + ( I − F ) d } \begin{align}
\bm{y} &= \bm{P}\{(\bm{I} - \bm{F}) + \bm{F}\bm{P}^{-1}_{\rm n} \bm{P})\}^{-1} \{\bm{u}^{\rm ref} + (\bm{I}-\bm{F})\bm{d}\}
\end{align} y = P {( I − F ) + F P n − 1 P ) } − 1 { u ref + ( I − F ) d } この制御系のノミナル出力は、
P = P n \bm{P}=\bm{P}_{\rm n} P = P n として次のようになる。
y = P n u r e f + P n ( I − F ) d \begin{align}
\bm{y} &= \bm{P}_{\rm n}\bm{u}^{\rm ref} + \bm{P}_{\rm n}(\bm{I}-\bm{F})\bm{d}
\end{align} y = P n u ref + P n ( I − F ) d この式より、外乱抑圧のノミナル性能は
F \bm{F} F の設計にのみ依存することが確認できる。外乱の周波数特性を考慮して
F \bm{F} F を設計することで、制御系に作用する外乱の影響を抑圧可能となる。ただし、外乱の特定のダイナミクスの完全な推定および抑圧を達成するためには、状態空間表現から外乱オブザーバを設計することが望ましい。
外乱オブザーバを用いた外乱抑圧制御系は、追従特性と外乱抑圧特性に対して独立の設計自由度を与えるため二自由度制御系となる。これは本制御系がフィードフォワード制御器およびフィードバック制御器を有する一般化二自由度制御系と等価な構造を持つことを示している。一般化二自由度制御系と等価な構造を得ることができれば、極零点配置解析やロバスト性解析などの伝統的な解析手法を活用することができる。ここでは
Youla-Kučera パラメトリゼーション より導出される安定化フィードバック制御器を介して二自由度制御系の構造的特徴を確認し、外乱オブザーバの作用について考える。
プラントを
P \bm{P} P , 入出力および外乱を
u , y , d \bm{u}, \bm{y}, \bm{d} u , y , d として、制御対象が以下のように表現される場合について考える。
y = P ( u + d ) \begin{align}
\bm{y} = \bm{P}(\bm{u} + \bm{d})
\end{align} y = P ( u + d ) ただし,プラントの右既約分解および左既約分解が次のように表されるものとする。
P = N D − 1 = D ~ − 1 N ~ \begin{align}
\bm{P} = \bm{N}\bm{D}^{-1} = \tilde{\bm{D}}^{-1}\tilde{\bm{N}}
\end{align} P = N D − 1 = D ~ − 1 N ~ Youla-Kučera パラメトリゼーションより,モデル誤差の存在しないノミナルプラント
P \bm{P} P を安定化するフィードバック制御器
C 0 \bm{C}_{0} C 0 が存在する場合に,ノミナルプラントに対する安定化フィードバック制御器群
C \bm{C} C は以下のように表される。
C 0 = Y ~ − 1 X ~ C = ( Y ~ − Q N ~ ) − 1 ( X ~ + Q D ~ ) \begin{align}
\bm{C}_{0} &= \tilde{\bm{Y}}^{-1} \tilde{\bm{X}} \\
\bm{C} &= (\tilde{\bm{Y}} - \bm{Q}\tilde{\bm{N}})^{-1} (\tilde{\bm{X}} + \bm{Q}\tilde{\bm{D}})
\end{align} C 0 C = Y ~ − 1 X ~ = ( Y ~ − Q N ~ ) − 1 ( X ~ + Q D ~ ) ただし,
C 0 \bm{C}_{0} C 0 を構成するパラメータ
X ~ , Y ~ \tilde{\bm{X}}, \tilde{\bm{Y}} X ~ , Y ~ は以下のBézout 等式を満たすものとし,
Q \bm{Q} Q は安定かつプロパなフリーパラメータとする。
[ Y ~ X ~ − N ~ D ~ ] [ D − X N Y ] = I \begin{align}
\begin{bmatrix}
\tilde{\bm{Y}} & \tilde{\bm{X}} \\ -\tilde{\bm{N}} & \tilde{\bm{D}}
\end{bmatrix}
\begin{bmatrix}
\bm{D} & -\bm{X} \\ \bm{N} & \bm{Y}
\end{bmatrix}
= \bm{I}
\end{align} [ Y ~ − N ~ X ~ D ~ ] [ D N − X Y ] = I ここで、このフィードバック制御器
C \bm{C} C を用いて二自由度制御系を構築した場合について考える。
この制御系の制御入力は,フィードフォワード制御入力
u f f \bm{u}_{\rm ff} u ff およびフィードバック制御入力
u f b \bm{u}_{\rm fb} u fb を合わせて次のように記述される。
u = u f f + u f b u f f ≡ D K r u f b ≡ ( Y ~ − Q N ~ ) − 1 ( X ~ + Q D ~ ) ( N K r − y ) \begin{align}
\bm{u} &= \bm{u}_{\rm ff} + \bm{u}_{\rm fb} \\
\bm{u}_{\rm ff} &\equiv \bm{D}\bm{K}\bm{r} \\
\bm{u}_{\rm fb} &\equiv (\tilde{\bm{Y}} - \bm{Q}\tilde{\bm{N}})^{-1} (\tilde{\bm{X}} + \bm{Q}\tilde{\bm{D}})(\bm{N}\bm{K}\bm{r}-\bm{y})
\end{align} u u ff u fb = u ff + u fb ≡ D K r ≡ ( Y ~ − Q N ~ ) − 1 ( X ~ + Q D ~ ) ( N K r − y ) この制御入力
u , u f b \bm{u}, \bm{u}_{\rm fb} u , u fb は次の代数方程式を満たす。
u f b = Y ~ − 1 { Q N ~ u f b + ( X ~ + Q D ~ ) ( N K r − y ) } = Y ~ − 1 [ Q { N ~ ( u f b + D K r ) − D ~ y } + X ~ ( N K r − y ) ] = C 0 ( N K r − y ) + Y ~ − 1 Q ( N ~ u − D ~ y ) ∴ u = D K r + C 0 ( N K r − y ) + Y ~ − 1 Q ( N ~ u − D ~ y ) \begin{align}
\bm{u}_{\rm fb} &= \tilde{\bm{Y}}^{-1} \{ \bm{Q}\tilde{\bm{N}}\bm{u}_{\rm fb} + (\tilde{\bm{X}} + \bm{Q}\tilde{\bm{D}})(\bm{N}\bm{K}\bm{r}-\bm{y}) \} \\
&= \tilde{\bm{Y}}^{-1} [ \bm{Q}\{\tilde{\bm{N}}(\bm{u}_{\rm fb} + \bm{D}\bm{K}\bm{r}) - \tilde{\bm{D}}\bm{y}\} + \tilde{\bm{X}}(\bm{N}\bm{K}\bm{r}-\bm{y}) ] \\
&= \bm{C}_{0}(\bm{N}\bm{K}\bm{r}-\bm{y}) + \tilde{\bm{Y}}^{-1}\bm{Q} (\tilde{\bm{N}}\bm{u} - \tilde{\bm{D}}\bm{y}) \\
\therefore \bm{u} &= \bm{D}\bm{K}\bm{r} + \bm{C}_{0}(\bm{N}\bm{K}\bm{r}-\bm{y}) + \tilde{\bm{Y}}^{-1}\bm{Q} (\tilde{\bm{N}}\bm{u} - \tilde{\bm{D}}\bm{y}) \\
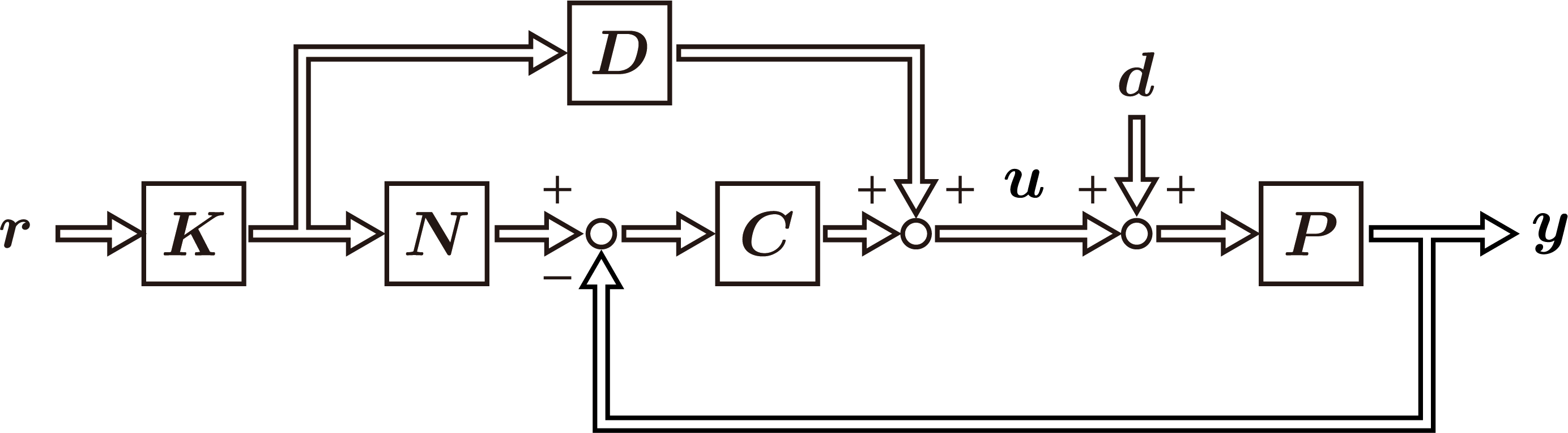
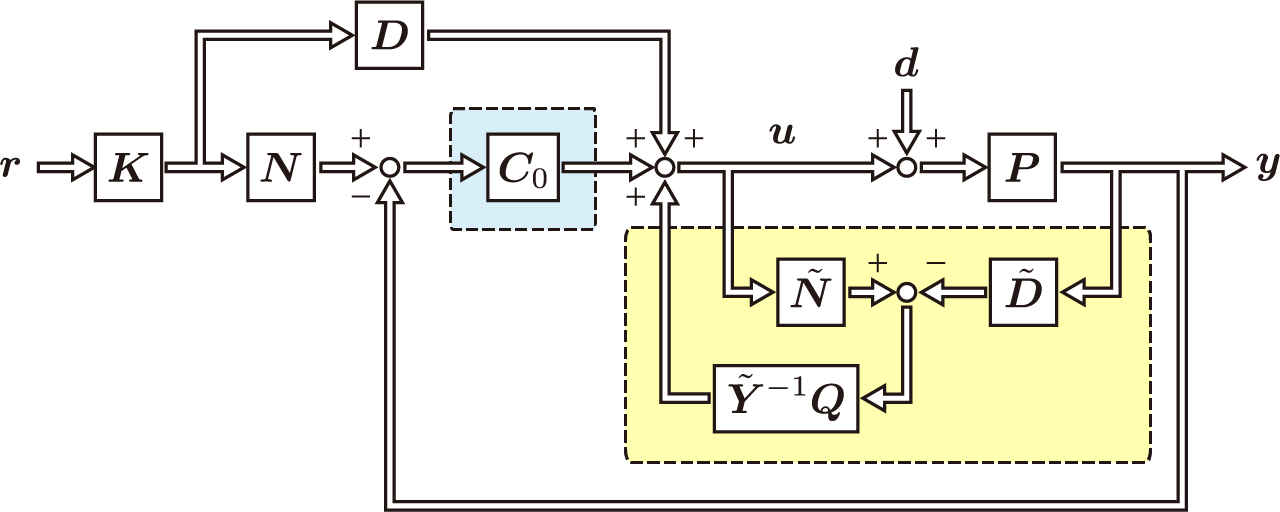
\end{align} u fb ∴ u = Y ~ − 1 { Q N ~ u fb + ( X ~ + Q D ~ ) ( N K r − y )} = Y ~ − 1 [ Q { N ~ ( u fb + D K r ) − D ~ y } + X ~ ( N K r − y )] = C 0 ( N K r − y ) + Y ~ − 1 Q ( N ~ u − D ~ y ) = D K r + C 0 ( N K r − y ) + Y ~ − 1 Q ( N ~ u − D ~ y ) この代数方程式より,一般化二自由度制御系の等価ブロック線図は以下のようになる。
これはフィードバック制御器
C 0 \bm{C}_{0} C 0 を持つ二自由度制御系に対し,フリーパラメータ
Q \bm{Q} Q によって決定される外乱抑圧機構が追加されたものと見ることができる。この追加機構に含まれる
N ~ u − D ~ y \tilde{\bm{N}}\bm{u} - \tilde{\bm{D}}\bm{y} N ~ u − D ~ y は外乱
d \bm{d} d の情報を含み,出力フィードバックによって推定外乱フィードバックが発生していることを示している。続いて,出力
y \bm{y} y の代数方程式より以下の解を得る。
y = P { D K r + C 0 ( N K r − y ) + Y ~ − 1 Q ( N ~ u − D ~ y ) + d } = P { ( P − 1 + C 0 ) N K r − C 0 y + ( I − Y ~ − 1 Q N ~ ) d } ∴ y = N K r + ( I + P C 0 ) − 1 P ( I − Y ~ − 1 Q N ~ ) d \begin{align}
\bm{y} &= \bm{P} \{ \bm{D}\bm{K}\bm{r} + \bm{C}_{0}(\bm{N}\bm{K}\bm{r}-\bm{y}) + \tilde{\bm{Y}}^{-1}\bm{Q} (\tilde{\bm{N}}\bm{u} - \tilde{\bm{D}}\bm{y}) + \bm{d} \} \\
&= \bm{P} \{ (\bm{P}^{-1} + \bm{C}_{0})\bm{N}\bm{K}\bm{r} - \bm{C}_{0}\bm{y} + (\bm{I} - \tilde{\bm{Y}}^{-1}\bm{Q}\tilde{\bm{N}}) \bm{d} \} \\
\therefore \bm{y} &= \bm{N}\bm{K}\bm{r} + (\bm{I}+\bm{P}\bm{C}_{0})^{-1} \bm{P} (\bm{I} - \tilde{\bm{Y}}^{-1}\bm{Q}\tilde{\bm{N}}) \bm{d}
\end{align} y ∴ y = P { D K r + C 0 ( N K r − y ) + Y ~ − 1 Q ( N ~ u − D ~ y ) + d } = P {( P − 1 + C 0 ) N K r − C 0 y + ( I − Y ~ − 1 Q N ~ ) d } = N K r + ( I + P C 0 ) − 1 P ( I − Y ~ − 1 Q N ~ ) d この解は外乱抑圧特性がフリーパラメータ
Q \bm{Q} Q によって設計可能であることを示している。このように,Youla-Kučera パラメトリゼーションによって導出されるフィードバック制御系は出力フィードバックと推定外乱フィードバックの両機構を含有する。異なる観点から,外乱オブザーバを用いた推定外乱フィードバックの導入は外乱抑圧特性の独立した設計自由度を与え,容易に二自由度制御系の実装可能とする。外乱オブザーバを用いた制御系は
C 0 = 0 \bm{C}_{0}=\bm{0} C 0 = 0 とした二自由度制御系と一致し,限定的な二自由度制御系を構築する。
外乱オブザーバを利用する利点として,Youla-Kučera パラメトリゼーションとは異なり外乱抑圧機構を直接かつ明示的に設置することができるため,外乱抑圧特性の設計が容易となることが挙げられる。外乱オブザーバは外側ループのフィードバック制御器と独立して設計可能であり,内部ループで二自由度制御系を構築することから追従特性を確立しつつ外乱抑圧特性を向上することができるため,階層的設計において設計が容易となる。特に運動制御では加速度次元の二自由度制御を実現し,位置制御系,速度制御系,および力制御系の設計を簡潔にする役割を持つ。
外乱オブザーバによる外乱抑圧機構を有する制御系は、以下のフィードバック制御器
C d \bm{C}_{\rm d} C d を持つ二自由度制御系と等価な構造を持つ。これは Youla-Kučera パラメトリゼーション により与えられる安定化制御器
C \bm{C} C のうち、
X ~ = 0 \tilde{\bm{X}}=\bm{0} X ~ = 0 かつ
Y ~ = D − 1 \tilde{\bm{Y}}=\bm{D}^{-1} Y ~ = D − 1 としたものである。
C d = ( D − 1 − Q N ~ ) − 1 Q D ~ \begin{align}
\bm{C}_{\rm d} &= (\bm{D}^{-1}-\bm{Q}\tilde{\bm{N}})^{-1}\bm{Q}\tilde{\bm{D}}
\end{align} C d = ( D − 1 − Q N ~ ) − 1 Q D ~ ここで
L ≡ D Q N ~ \bm{L}\equiv \bm{D}\bm{Q}\tilde{\bm{N}} L ≡ D Q N ~ を導入し、上記の表現を簡略化する。
C d = ( I − L ) − 1 L P − 1 \begin{align}
\bm{C}_{\rm d} &= (\bm{I}-\bm{L})^{-1}\bm{L}\bm{P}^{-1}
\end{align} C d = ( I − L ) − 1 L P − 1 以上より、感度関数
S \bm{S} S および相補感度関数
T \bm{T} T は次のように記述される。
S = ( I + P C d ) − 1 = I − P L P − 1 T = I − S = P L P − 1 \begin{align}
\bm{S} &= (\bm{I}+\bm{P}\bm{C}_{\rm d})^{-1} = \bm{I} - \bm{P}\bm{L}\bm{P}^{-1} \\
\bm{T} &= \bm{I} - \bm{S} = \bm{P}\bm{L}\bm{P}^{-1}
\end{align} S T = ( I + P C d ) − 1 = I − P L P − 1 = I − S = P L P − 1 ロバスト性に加えて、モデル変動時の実際の伝達特性を確認する。プラント
P \bm{P} P に対してノミナルモデルを
P n \bm{P}_{\rm n} P n として外乱オブザーバが設計され、かつ外乱抑圧機構が構成されるとき、等価フィードバック制御器
C d n \bm{C}_{\rm dn} C dn は次のように表される。
C d n = ( I − L n ) − 1 L n P n − 1 L n ≡ D n Q N ~ n \begin{align}
\bm{C}_{\rm dn} &= (\bm{I}-\bm{L}_{\rm n})^{-1}\bm{L}_{\rm n}\bm{P}_{\rm n}^{-1} \\
\bm{L}_{\rm n} &\equiv \bm{D}_{\rm n}\bm{Q}\tilde{\bm{N}}_{\rm n}
\end{align} C dn L n = ( I − L n ) − 1 L n P n − 1 ≡ D n Q N ~ n ただし、ノミナルモデルの右既約分解および左既約分解が次のように表されるものとする。
P n = N n D n − 1 = D ~ n − 1 N ~ n \begin{align}
\bm{P}_{\rm n} = \bm{N}_{\rm n}\bm{D}_{\rm n}^{-1} = \tilde{\bm{D}}_{\rm n}^{-1}\tilde{\bm{N}}_{\rm n}
\end{align} P n = N n D n − 1 = D ~ n − 1 N ~ n このとき、出力
y \bm{y} y は次のように表される。
y = T r y r + T d y d T r y ≡ P { ( I − L n ) + L n P n − 1 P } − 1 P n − 1 T d y ≡ P { ( I − L n ) + L n P n − 1 P } − 1 ( I − L n ) \begin{align}
\bm{y} &= \bm{T}_{ry}\bm{r} + \bm{T}_{dy}\bm{d} \\
\bm{T}_{ry} &\equiv \bm{P} \{ (\bm{I}-\bm{L}_{\rm n}) + \bm{L}_{\rm n}\bm{P}_{\rm n}^{-1}\bm{P} \}^{-1}\bm{P}_{\rm n}^{-1} \\
\bm{T}_{dy} &\equiv \bm{P} \{ (\bm{I}-\bm{L}_{\rm n}) + \bm{L}_{\rm n}\bm{P}_{\rm n}^{-1}\bm{P} \}^{-1}(\bm{I} - \bm{L}_{\rm n})
\end{align} y T ry T d y = T ry r + T d y d ≡ P {( I − L n ) + L n P n − 1 P } − 1 P n − 1 ≡ P {( I − L n ) + L n P n − 1 P } − 1 ( I − L n ) この伝達特性は
L n \bm{L}_{\rm n} L n の通過帯域および遮断帯域に分けて考えることで簡易的に確認することができる。通過帯域では
L n = I \bm{L}_{\rm n}=\bm{I} L n = I として以下を得る。
T r y = P ( P n − 1 P ) − 1 P n − 1 = I T d y = P ( P n − 1 P ) − 1 ( I − L n ) = P n − 1 ( I − L n ) \begin{align}
\bm{T}_{ry} &= \bm{P} ( \bm{P}_{\rm n}^{-1}\bm{P} )^{-1}\bm{P}_{\rm n}^{-1} = \bm{I}\\
\bm{T}_{dy} &= \bm{P} ( \bm{P}_{\rm n}^{-1}\bm{P} )^{-1}(\bm{I} - \bm{L}_{\rm n}) = \bm{P}_{\rm n}^{-1}(\bm{I} - \bm{L}_{\rm n})
\end{align} T ry T d y = P ( P n − 1 P ) − 1 P n − 1 = I = P ( P n − 1 P ) − 1 ( I − L n ) = P n − 1 ( I − L n ) 遮断帯域では
L n = 0 \bm{L}_{\rm n}=\bm{0} L n = 0 として以下を得る。
T r y = P P n − 1 T d y = P ( I − L n ) \begin{align}
\bm{T}_{ry} &= \bm{P} \bm{P}_{\rm n}^{-1} \\
\bm{T}_{dy} &= \bm{P} (\bm{I} - \bm{L}_{\rm n})
\end{align} T ry T d y = P P n − 1 = P ( I − L n ) このように伝達特性はモデル誤差に起因して周波数帯域依存の変動を伴い、ノミナル伝達特性に位相補償特性を追加した特性を示す。