DigitalServo

Blog

About

Library

    線形制御系設計

    線形システムの表現
    線形システムの特性解析
    制御器設計
    観測器設計

    モーションコントロール

    加速度制御
    剛体の姿勢制御

    モータドライブ

    駆動制御法
    磁極位置推定法

    システム同定

    ホワイトボックスモデル

最小次元オブザーバ

同一次元オブザーバは状態空間表現の全状態量の推定を行うため、状態量の増加に伴いオブザーバの設計が複雑化する。これに対して測定可能な状態量を信頼可能な既知情報とし、測定できない状態量のみを推定するものを最小次元オブザーバと呼ぶ。ここでは最小次元オブザーバの構成方法について述べる。

低次元化システムの導出

最小次元オブザーバでは測定可能な状態量を既知情報として「未知状態量に関する低次元化された状態空間表現」を導出し、その状態空間モデルに対して同一次元オブザーバを設計することで未知状態量を推定する。はじめに、測定可能な状態量を z\bm{z}、未知状態量を ξ\bm{\xi} としてシステムに関する状態空間モデルを記述する。
ddt[ξz]=[A11A12A21A22][ξz]+[B1B2]u+[H1H2]vy=z+w\begin{align} \frac{d}{dt}\begin{bmatrix} \bm{\xi} \\ \bm{z} \end{bmatrix} &= \begin{bmatrix} \bm{A}_{11} & \bm{A}_{12} \\ \bm{A}_{21} & \bm{A}_{22} \end{bmatrix}\begin{bmatrix} \bm{\xi} \\ \bm{z} \end{bmatrix} + \begin{bmatrix} \bm{B}_{1} \\ \bm{B}_{2} \end{bmatrix}\bm{u} + \begin{bmatrix} \bm{H}_{1} \\ \bm{H}_{2} \end{bmatrix}\bm{v} \\ \bm{y}&=\bm{z}+\bm{w} \end{align}
ただし、u,y,v,w\bm{u}, \bm{y}, \bm{v}, \bm{w} はそれぞれ入力、出力、プロセス雑音、観測雑音を表す。整理された状態空間表現から、以下の等式を得る。
{ξ˙=A11ξ+(A12z+B1u)+H1vz˙−A22z−B2u=A21ξ+H2v\begin{align} & \left\{ \begin{matrix} \dot{\bm{\xi}}=\bm{A}_{11}\bm{\xi}+(\bm{A}_{12}\bm{z}+\bm{B}_{1}\bm{u})+\bm{H}_{1}\bm{v} \\ \dot{\bm{z}}-\bm{A}_{22}\bm{z}-\bm{B}_{2}\bm{u}=\bm{A}_{21}\bm{\xi} +\bm{H}_{2}\bm{v} \end{matrix} \right. \end{align}
ここで、既知量 u,z\bm{u}, \bm{z} を用いて新しい予測可能量 U,Y\bm{U}, \bm{Y} を導入する。
U≡A12z+B1uY≡z˙−A22z−B2u\begin{align} \bm{U} &\equiv \bm{A}_{12}\bm{z}+\bm{B}_{1}\bm{u}\\ \bm{Y} &\equiv \dot{\bm{z}}-\bm{A}_{22}\bm{z}-\bm{B}_{2}\bm{u} \end{align}
これにより、未知状態量に関して低次元化された状態空間表現が得られる。
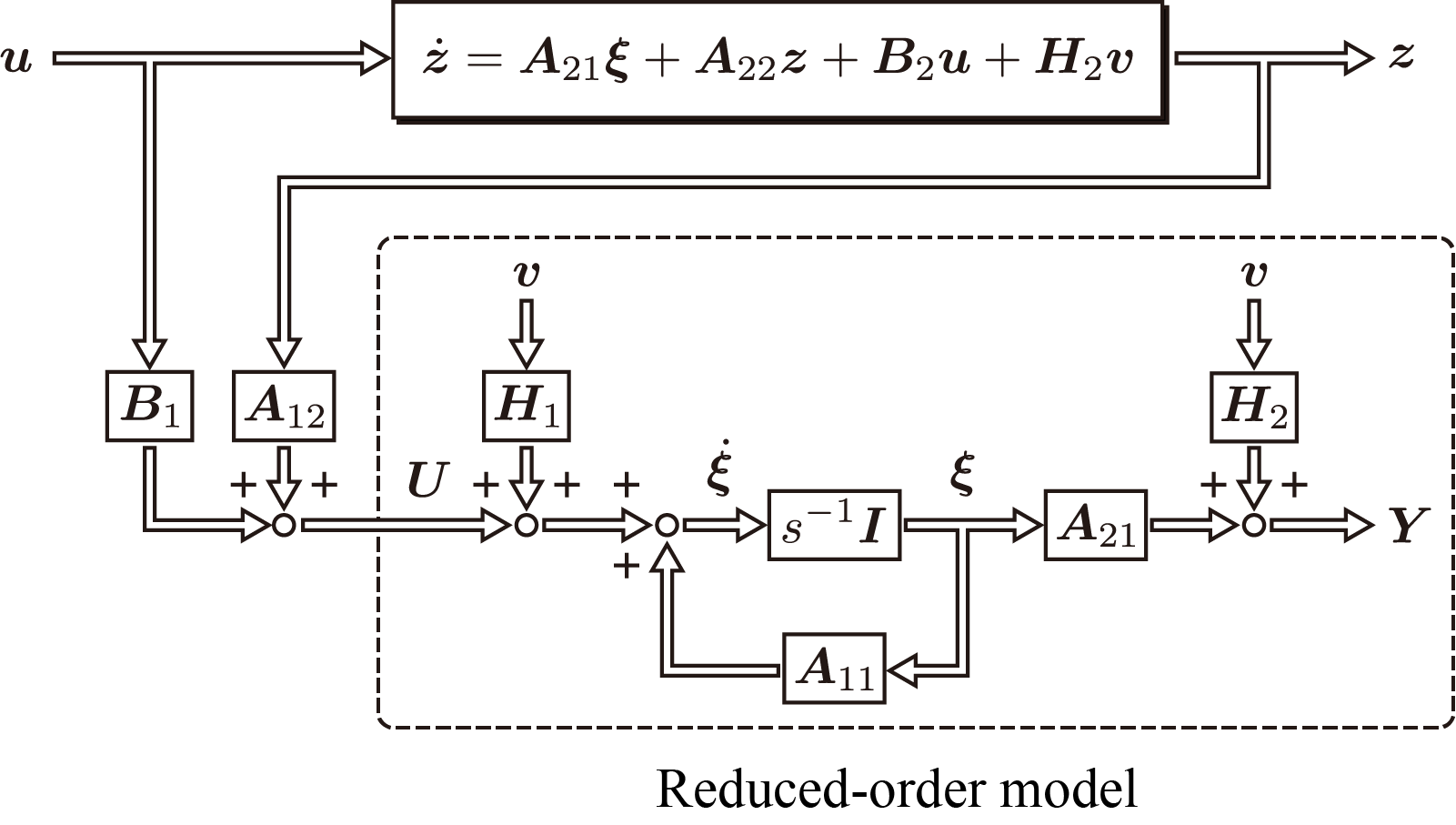
{ξ˙=A11ξ+U+H1vY=A21ξ+H2v\begin{align} & \left\{ \begin{matrix} \dot{\bm{\xi}}=\bm{A}_{11}\bm{\xi}+\bm{U} +\bm{H}_{1}\bm{v}\\ \bm{Y}=\bm{A}_{21}\bm{\xi} +\bm{H}_{2}\bm{v}\end{matrix} \right. \\ \end{align}
この表現において U,Y\bm{U}, \bm{Y} はそれぞれ入力および出力として作用し、A11,A21\bm{A}_{11}, \bm{A}_{21} はそれぞれシステム行列および観測行列の役割を果たす。このシステムのブロック線図は以下のようになる。
image is here

設計方法

低次元化された状態空間表現における入出力 U,Y\bm{U}, \bm{Y} に対して、既知情報を用いた予測値を Uˉ,Yˉ\bar{\bm{U}}, \bar{\bm{Y}} として次のように設計する。
Uˉ=An12y+Bn1uYˉ=y˙−An22y−Bn2u\begin{align} \bar{\bm{U}}&=\bm{A}_{{\rm n}12}\bm{y}+\bm{B}_{{\rm n}1}\bm{u} \\ \bar{\bm{Y}}&=\dot{\bm{y}}-\bm{A}_{{\rm n}22}\bm{y}-\bm{B}_{{\rm n}2}\bm{u} \end{align}
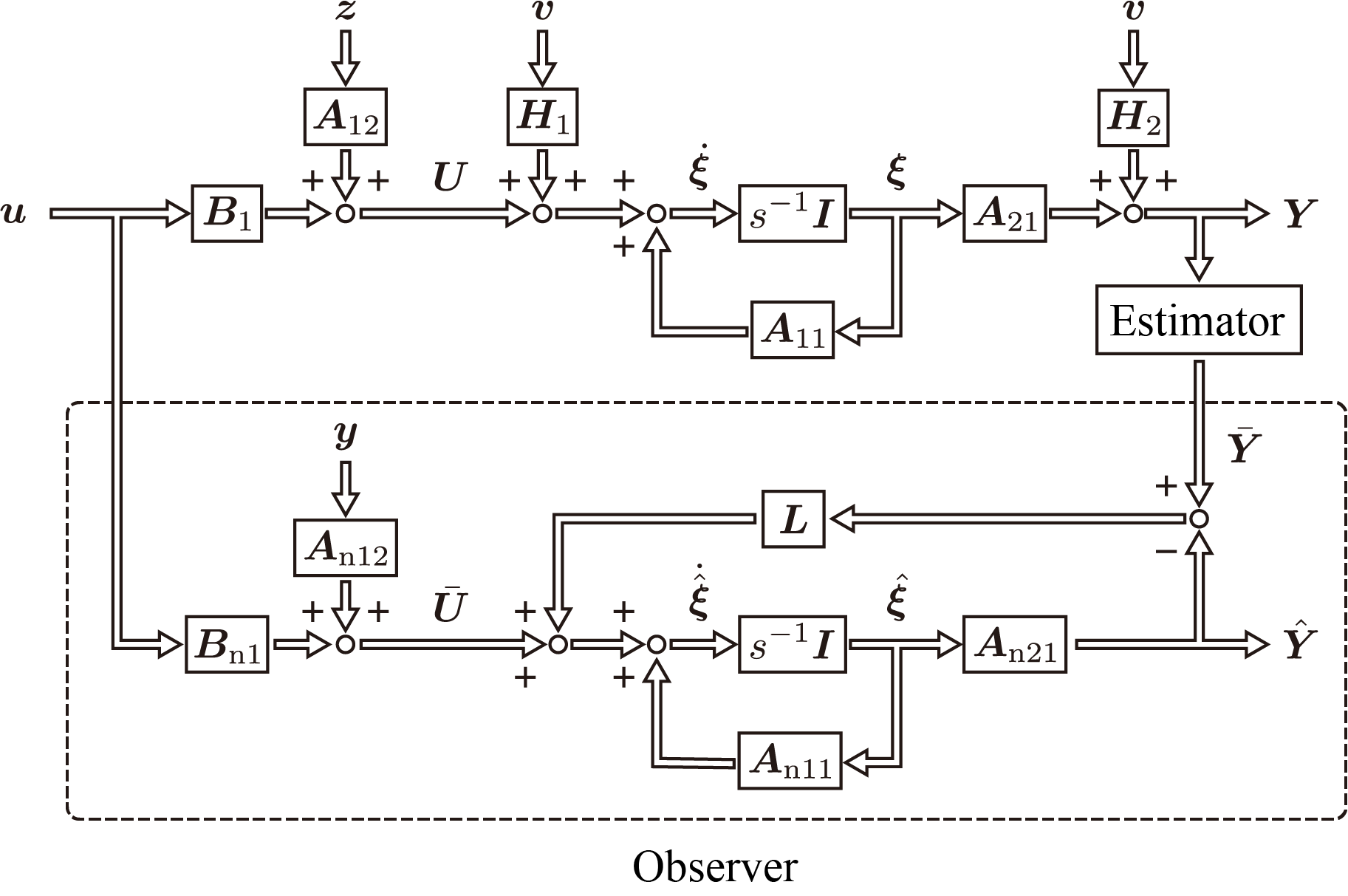
ただし、下添字 n_{\rm n} は公称値を表し、予測には z\bm{z} の観測値である y\bm{y} を使用することに留意する。このモデルを用いて、低次元化システムに対する同一次元オブザーバを次のように構成する。
image is here
このオブザーバを最小次元オブザーバと呼ぶ。このとき、未知状態量 ξ\bm{\xi} に関する推定式は次のようになる。
ξ˙^=An11ξ^+Uˉ+L(Yˉ−Y^)Y^=An21ξ^\begin{align} \hat{\dot{\bm{\xi}}} &= \bm{A}_{{\rm n}11}\hat{\bm{\xi}}+\bar{\bm{U}}+\bm{L}(\bar{\bm{Y}}-\hat{\bm{Y}})\\ \hat{\bm{Y}} &= \bm{A}_{{\rm n}21}\hat{\bm{\xi}} \end{align}
この推定式を整理することにより、以下を得る。
ξ˙^=An11ξ^+Uˉ+L(Yˉ−Y^)=An11ξ^+(An12y+Bn1u)+L((y˙−An22y−Bn2u)−An21ξ^)=(An11−LAn21)ξ^+(An12−LAn22)y+(Bn1−LBn2)u+Ly˙=Tξξ^+Tuu+Tyy+Ly˙\begin{align} \hat{\dot{\bm{\xi}}}&=\bm{A}_{{\rm n}11}\hat{\bm{\xi}}+\bar{\bm{U}}+\bm{L}(\bar{\bm{Y}}-\hat{\bm{Y}})\\ &=\bm{A}_{{\rm n}11}\hat{\bm{\xi}}+(\bm{A}_{{\rm n}12}\bm{y}+\bm{B}_{{\rm n}1}\bm{u})+\bm{L}((\dot{\bm{y}}-\bm{A}_{{\rm n}22}\bm{y}-\bm{B}_{{\rm n}2}\bm{u})-\bm{A}_{{\rm n} 21}\hat{\bm{\xi}}) \\ &=(\bm{A}_{{\rm n}11}-\bm{L}\bm{A}_{{\rm n} 21})\hat{\bm{\xi}}+(\bm{A}_{{\rm n}12}-\bm{L}\bm{A}_{{\rm n}22})\bm{y}+(\bm{B}_{{\rm n}1}-\bm{L}\bm{B}_{{\rm n}2})\bm{u}+\bm{L}\dot{\bm{y}}\\ &=\bm{T}_{\xi}\hat{\bm{\xi}} + \bm{T}_{u}\bm{u} + \bm{T}_{y}\bm{y}+\bm{L}\dot{\bm{y}} \end{align}
ただし、Tξ,Tu,Ty\bm{T}_{\xi}, \bm{T}_{u}, \bm{T}_{y} は係数行列を表し、以下のように定義する。
Tξ≡An11−LAn21Tu≡Bn1−LBn2Ty≡An12−LAn22\begin{align} \bm{T}_{\xi} &\equiv \bm{A}_{{\rm n}11}-\bm{L}\bm{A}_{{\rm n} 21}\\ \bm{T}_{u} &\equiv \bm{B}_{{\rm n}1}-\bm{L}\bm{B}_{{\rm n}2}\\ \bm{T}_{y} &\equiv \bm{A}_{{\rm n}12}-\bm{L}\bm{A}_{{\rm n}22} \end{align}
この表現は右辺に出力 y\bm{y} の微分値を含むため、実装が困難となる。そのため、次の変数変換によって本問題を回避する。
P≡ξ^−Ly\begin{align} \bm{P}&\equiv\hat{\bm{\xi}}-\bm{L}\bm{y} \end{align}
このとき、変数 P\bm{P} は次のように求めることができる。
P˙=Tξξ^+Tuu+Tyy=TξP+Tuu+(TξL+Ty)y∴P=(sI−Tξ)−1{Tuu+(TξL+Ty)y}\begin{align} \dot{\bm{P}} &=\bm{T}_{\xi}\hat{\bm{\xi}} + \bm{T}_{u}\bm{u} + \bm{T}_{y}\bm{y}\\ &=\bm{T}_{\xi}\bm{P}+\bm{T}_{u}\bm{u} + (\bm{T}_{\xi}\bm{L}+\bm{T}_{y})\bm{y}\\ \therefore \bm{P}&=(s\bm{I}-\bm{T}_{\xi})^{-1}\left\{ \bm{T}_{u}\bm{u} + (\bm{T}_{\xi}\bm{L}+\bm{T}_{y})\bm{y} \right\} \end{align}
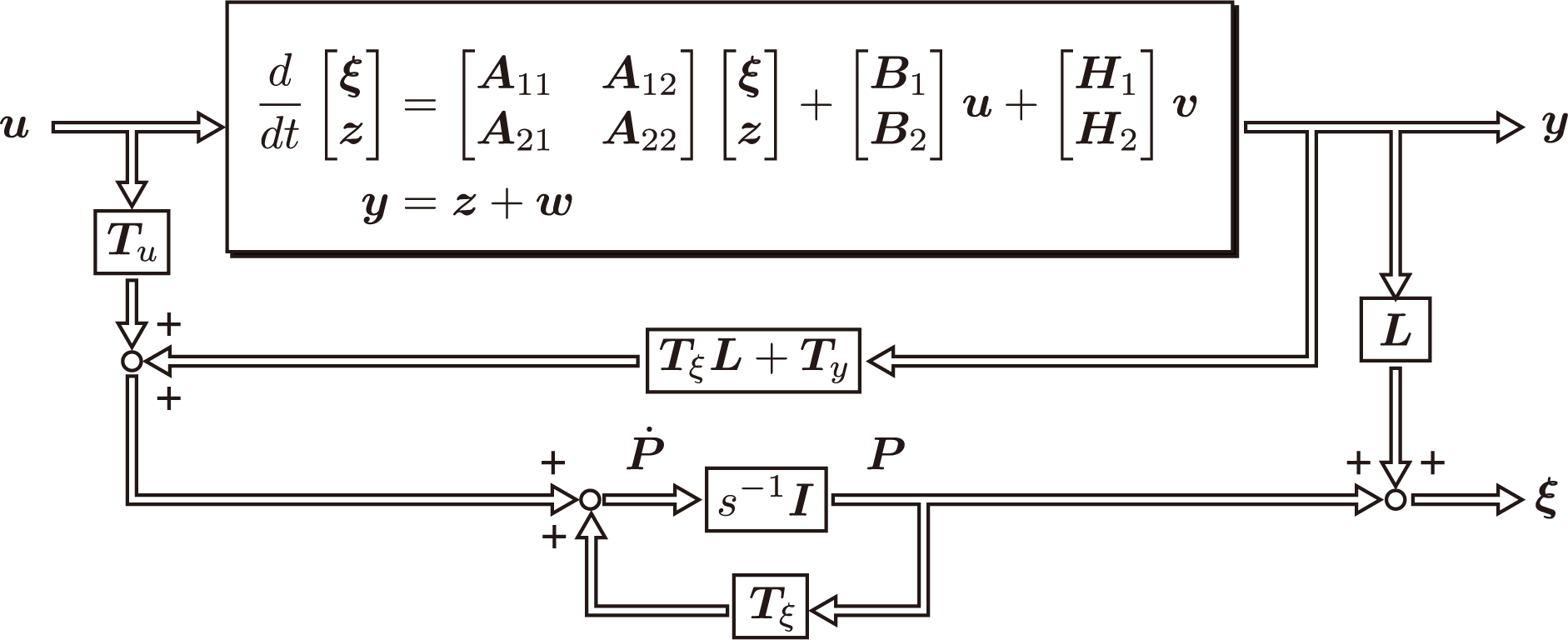
以上より、最小次元オブザーバの等価構造として以下の表現を得る。本形式はすべてのブロックがプロパであり、実装に適した形式となる。
image is here

動作解析

以下では便宜上、モデル化誤差のない状態空間表現モデルによって最小次元オブザーバが構築されたものとし、プロセス雑音および観測雑音が存在しないものとする。
[AnBnHy]=[AB0z]\begin{align} \begin{bmatrix} \bm{A}_{\rm n} & \bm{B}_{\rm n} & \bm{H} & \bm{y} \end{bmatrix} &= \begin{bmatrix} \bm{A} & \bm{B} & \bm{0} & \bm{z} \end{bmatrix} \end{align}
解析的な観点に立脚すれば、未知状態量の推定式は次のように記述される。
ξ^=(sI−Tξ)−1{Tuu+(TξL+Ty)y}+Ly=(sI−Tξ)−1[Tuu+{(TξL+Ty)+(sI−Tξ)L}y]=(sI−Tξ)−1{Tuu+(sL+Ty)y}\begin{align} \hat{\bm{\xi}}& =(s\bm{I}-\bm{T}_{\xi})^{-1}\left\{ \bm{T}_{u}\bm{u} + (\bm{T}_{\xi}\bm{L}+\bm{T}_{y})\bm{y} \right\} + \bm{L}\bm{y} \\ &=(s\bm{I}-\bm{T}_{\xi})^{-1} \left[ \bm{T}_{u} \bm{u} + \{(\bm{T}_{\xi}\bm{L}+\bm{T}_{y}) + (s\bm{I}-\bm{T}_{\xi})\bm{L}\}\bm{y} \right] \\ &=(s\bm{I}-\bm{T}_{\xi})^{-1} \left\{ \bm{T}_{u} \bm{u} + (s\bm{L} + \bm{T}_{y})\bm{y} \right\} \\ \end{align}
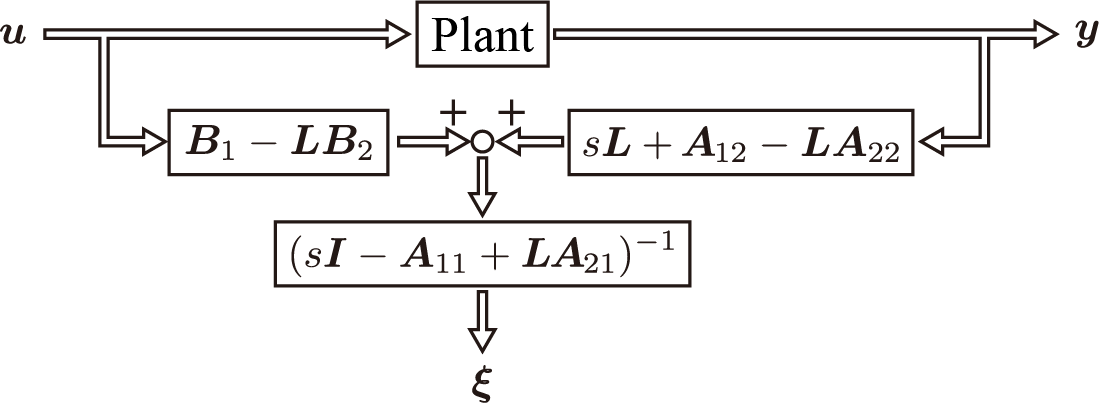
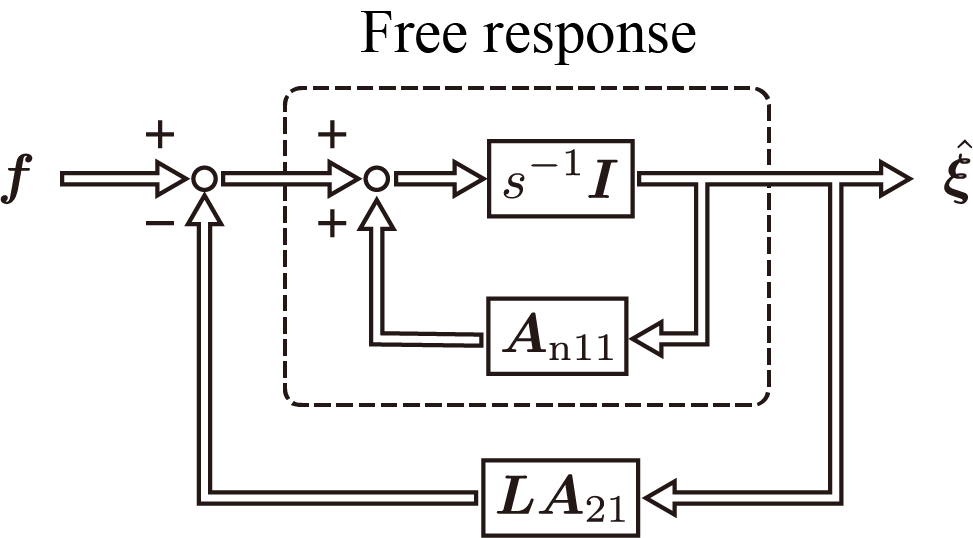
また、上式よりブロック線図を用いた表現は次のようになる。
image is here
このブロック線図を確認すると、最小次元オブザーバが状態量抽出部とフィルタリング部によって構成されていることがわかる。抽出信号を f\bm{f}、フィルタを g\bm{g} として以下のように記述する。
f≡Tuu+(sL+Ty)yg≡(sI−Tξ)−1\begin{align} \bm{f} &\equiv \bm{T}_{u} \bm{u} + (s\bm{L} + \bm{T}_{y})\bm{y}\\ \bm{g} &\equiv(s\bm{I}-\bm{T}_{\xi})^{-1} \end{align}
ここで、f\bm{f} について整理することで以下を得る。
f=(B1u+A12y)−L(B2u−sz+A22z)=(sξ−A11ξ)+LA21ξ≡uξ+LA21ξ\begin{align} \bm{f} &= (\bm{B}_{1}\bm{u} + \bm{A}_{12}\bm{y}) - \bm{L}(\bm{B}_{2}\bm{u} - s\bm{z} + \bm{A}_{22}\bm{z}) \\ &= (s\bm{\xi} - \bm{A}_{11}\bm{\xi}) + \bm{L}\bm{A}_{21}\bm{\xi} \\ &\equiv \bm{u}_{\xi} + \bm{L}\bm{A}_{21}\bm{\xi} \end{align}
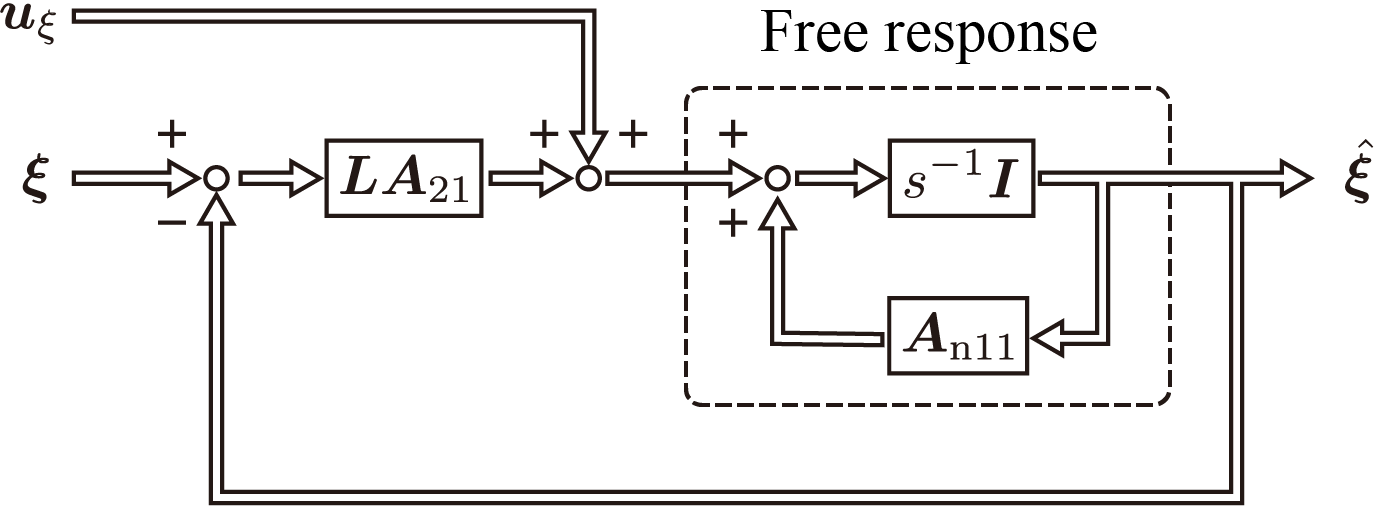
未知状態量 ξ\bm{\xi} の自由応答のダイナミクスが ξ˙=A11ξ\dot{\bm{\xi}}=\bm{A}_{11}\bm{\xi} と記述されることを考慮すると、右辺第一項 uξ\bm{u}_{\xi} は未知状態量 ξ\bm{\xi} のシステムに対する外因性入力と見ることができる。続いて、g\bm{g} についてブロック線図を用いて以下のように表現する。
image is here
この表現より、フィルタリング部は未知状態量 ξ\bm{\xi} のダイナミクスを考慮した更新系とオブザーバフィードバックによって構成されると見ることができる。以上の観点を基に、推定式 ξ^=gf\hat{\bm{\xi}}=\bm{g}\bm{f} を整理する。
g−1ξ^=f⇔sξ^=uξ+A11ξ^+LA21(ξ−ξ^)\begin{align} \bm{g}^{-1}\hat{\bm{\xi}} &= \bm{f}\\ \Leftrightarrow s\hat{\bm{\xi}} &= \bm{u}_{\xi} + \bm{A}_{11}\hat{\bm{\xi}}+ \bm{L}\bm{A}_{21} (\bm{\xi} - \hat{\bm{\xi}}) \\ \end{align}
これをブロック線図を用いて表現すると、二自由度制御系と等価の表現を得る。
image is here
これにより、モデル化誤差や雑音の影響を抑制して状態推定を行うことができる。ただし、ξ\bm{\xi} は固有のダイナミクス (生成モデル) を持つことから、内部モデル原理の観点よりAn11=A11\bm{A}_{\rm n11}=\bm{A}_{11} が成立しない場合には推定誤差の 0\bm{0} への収束を保証することはできない。

CONTENTS

© DigitalServo