DigitalServo

Blog

About

Library

    線形制御系設計

    線形システムの表現
    線形システムの特性解析
    制御器設計
    観測器設計

    モーションコントロール

    加速度制御
    剛体の姿勢制御

    モータドライブ

    駆動制御法
    磁極位置推定法

    システム同定

    ホワイトボックスモデル

ボード線図を用いた周波数解析

ボード線図は周波数伝達関数の振幅・位相を周波数を横軸として描画するものであり、システムの入出力における増幅率と位相変化量を周波数ごとに確認することができる。閉ループ伝達関数のボード線図はシステムの応答性を確認するために使用され、開ループもしくは一巡伝達関数のボード線図は閉ループ系の安定性を判別するために使用することができる。

描画方法

周波数伝達関数 G(jω)G(j\omega) に対して、振幅特性 gg および位相特性 ϕ\phi は次のように表される。
g(ω)=∣G(jω)∣ϕ(ω)=∠G(jω)\begin{align} g(\omega) &= |G(j\omega)| \\ \phi(\omega) &= \angle G(j\omega) \end{align}
ボード線図では縦軸の振幅および位相をそれぞれデジベル単位、度もしくはラジアン単位で表記し、横軸を対数スケールで表示する。そのため、振幅特性について次の単位変換を行う。
g(ω)=20log⁡10∣G(jω)∣ [dB]\begin{align} g(\omega) &= 20\log_{10}|G(j\omega)| \ {\rm [dB]} \end{align}
この二つの特性に関して横軸を周波数としたグラフを描画したものがボード線図となる。

一次遅れ系のボード線図

一次遅れ系の伝達関数について考える。
G(s)=ωns+ωn\begin{align} G(s)=\frac{\omega_{\rm n}}{s+\omega_{\rm n}} \end{align}
ただし、ωn\omega_{\rm n} は固有角周波数とする。ここで、周波数伝達関数は次のように記述される。
G(jω)=ωnωn+jω=ωnω2+ωn2e−jtan⁡−1(ωωn)\begin{align} G(j\omega)=\frac{\omega_{\rm n}}{\omega_{\rm n} + j\omega} = \frac{\omega_{\rm n}}{\sqrt{\omega^2 + \omega^2_{\rm n}}}e^{-j\tan^{-1} \left(\frac{\omega}{\omega_{\rm n}}\right) } \end{align}
したがって、伝達関数の振幅・位相特性は次式のように表される。
g(ω)=−10log⁡10(1+ω2ωn2)ϕ(ω)=−tan⁡−1(ωωn)\begin{align} g(\omega) &= - 10 \log_{10} \left(1 + \frac{\omega^2}{\omega_{\rm n}^2} \right) \\ \phi(\omega) &= -\tan^{-1} \left( \frac{\omega}{\omega_{\rm n}} \right) \end{align}
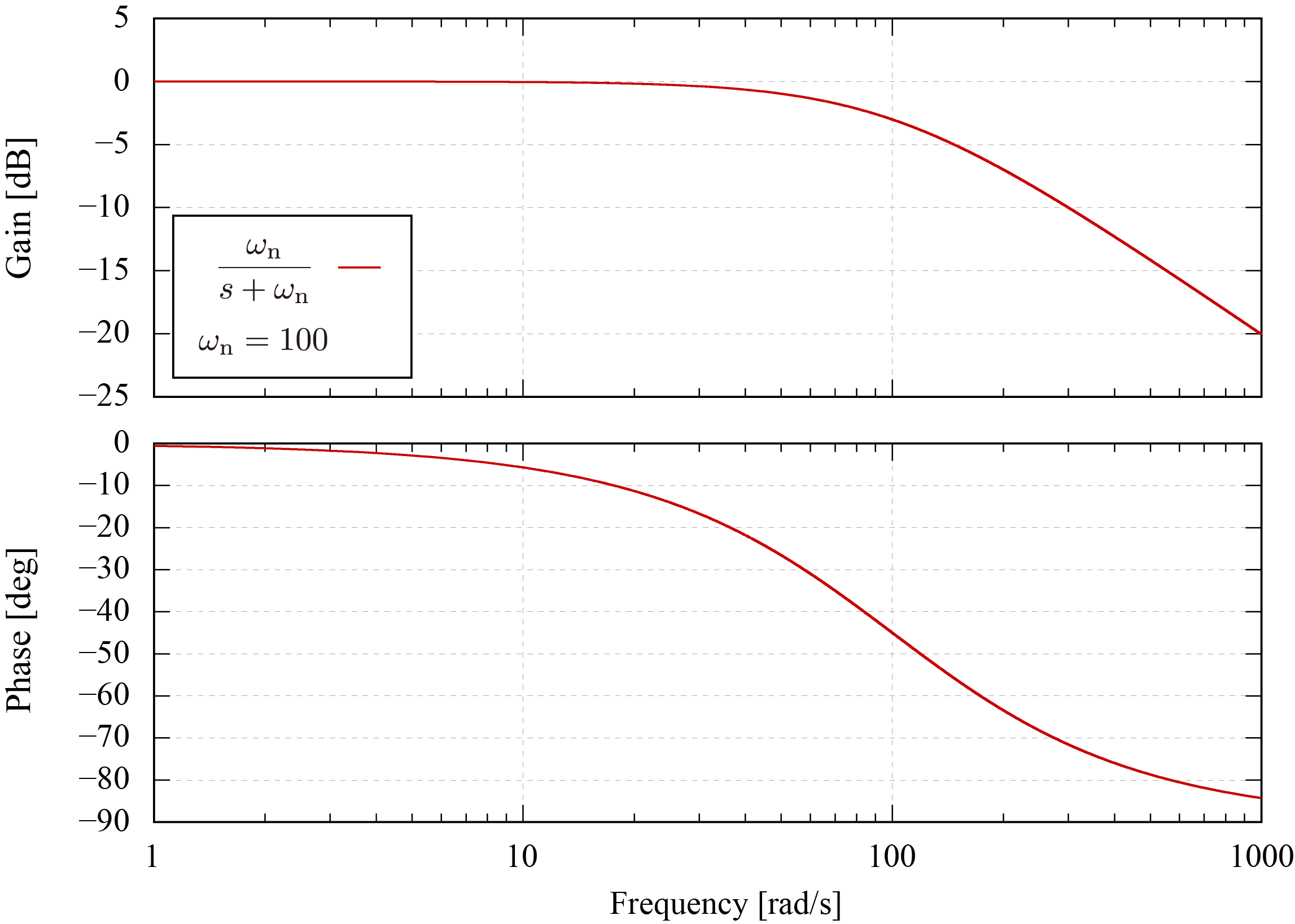
このモデルにおいて ωn=100\omega_{\rm n}=100 としたボード線図は下図のようになる。
image is here
固有角周波数における振幅・位相特性は以下のようになる。
g(ωn)=−10log⁡102≈−3.01ϕ(ωn)=−π4\begin{align} g(\omega_{\rm n}) &= - 10 \log_{10} 2 \approx -3.01\\ \phi(\omega_{\rm n}) &= - \frac{\pi}{4} \end{align}
振幅減衰量について 3 dB3\ {\rm dB} を基準として、それ以下の減衰量を持つ帯域を通過帯域、それ以上の減衰量を持つ帯域を遮断帯域と呼ぶ。この帯域を区切る周波数を遮断周波数と呼び、一次遅れ系では固有角周波数が遮断周波数となる。また、遮断帯域における振幅減衰量は単位デカードあたりの振幅減衰量で評価される。十分に高い周波数領域において、単位デカードあたりの変化量は次のように表される。
Δg=g(10ω)−g(ω)=−10log⁡10(1+100ω2ωn2)+10log⁡10(1+ω2ωn2)≈20(−log⁡10(10ωωn)+log⁡10(ωωn))=−20 [dB/dec]\begin{align} \Delta_{g} &= g(10\omega) - g(\omega) \\ &= - 10 \log_{10} \left(1 + \frac{100\omega^2}{\omega_{\rm n}^2} \right) + 10 \log_{10} \left(1 + \frac{\omega^2}{\omega_{\rm n}^2} \right) \\ &\approx 20 \left( -\log_{10} \left(\frac{10\omega}{\omega_{\rm n}} \right) + \log_{10} \left(\frac{\omega}{\omega_{\rm n}} \right) \right) \\ &= -20\ {\rm [dB/dec]} \end{align}

二次遅れ系のボード線図

零点を持たない場合

零点を持たない二次遅れ系の伝達関数について考える。
G(s)=ωn2s2+2ζωns+ωn2\begin{align} G(s)=\frac{\omega^2_{\rm n}}{s^2+2\zeta\omega_{\rm n}s + \omega^2_{\rm n}} \end{align}
ただし、ζ,ωn\zeta, \omega_{\rm n} は減衰率および固有角周波数とする。ここで、周波数伝達関数は次のように記述される。
G(jω)=ωn2(−ω2+ωn2)+j2ζωnω=ωn2ω4−2(1−2ζ2)ωn2ω2+ωn4ejϕ(ω)ϕ(ω)≡{−tan⁡−1(2ζωnωωn2−ω2)(ω≠ωn)−π2(ω=ωn)\begin{align} G(j\omega) &= \frac{\omega^2_{\rm n}}{(-\omega^2 + \omega^2_{\rm n}) + j2\zeta\omega_{\rm n}\omega}\\ &= \frac{\omega^2_{\rm n}}{\sqrt{\omega^4 - 2(1-2\zeta^2)\omega^2_{\rm n}\omega^2 + \omega_{\rm n}^4}}e^{j\phi(\omega) } \\ \phi(\omega) &\equiv \left\{ \begin{matrix} -\tan^{-1} \left(\frac{2\zeta\omega_{\rm n}\omega}{\omega^2_{\rm n} -\omega^2 }\right) & (\omega\neq\omega_{\rm n})\\ -\frac{\pi}{2} & (\omega = \omega_{\rm n}) \end{matrix} \right. \end{align}
したがって、伝達関数の振幅特性は次式のように表される。
g(ω)=−10log⁡10(1−2(1−2ζ2)ω2ωn2+ω4ωn4)\begin{align} g(\omega) &= - 10 \log_{10} \left(1 - 2(1-2\zeta^2) \frac{\omega^2}{\omega_{\rm n}^2}+\frac{\omega^4}{\omega_{\rm n}^4} \right) \end{align}
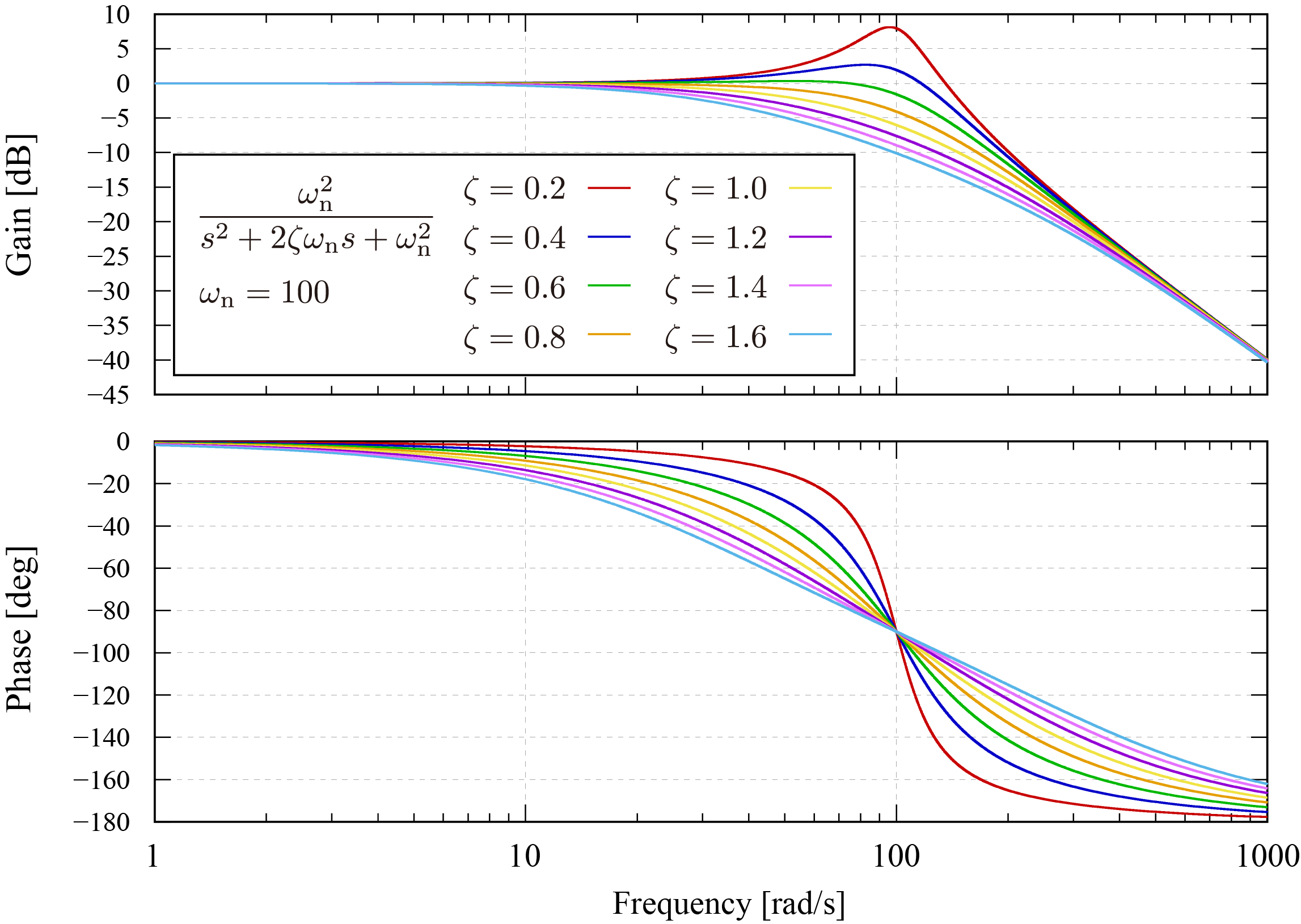
このモデルにおいて ωn=100\omega_{\rm n}=100 としたボード線図は下図のようになる。本図中では減衰率を 0.2∼1.60.2 \sim 1.6 の範囲で設定した場合の結果を示している。
image is here
固有角周波数における振幅・位相特性は以下のようになる。
g(ωn)=−20log⁡10(2ζ)ϕ(ωn)=−π2\begin{align} g(\omega_{\rm n}) &= - 20 \log_{10} \left( 2\zeta \right) \\ \phi(\omega_{\rm n}) &= - \frac{\pi}{2} \end{align}
固有角周波数における振幅変化量は、減衰率が 11 のとき −6 dB-6\ {\rm dB}、減衰率が 1/21/\sqrt{2} のとき −3 dB-3\ {\rm dB} となる。また、十分に高い周波数領域における単位デカードあたりの変化量は次のように表される。
Δg=g(10ω)−g(ω)≈10(−log⁡10(104ω4ωn4)+log⁡10(ω4ωn4))=−40 [dB/dec]\begin{align} \Delta_{g} &= g(10\omega) - g(\omega) \\ &\approx 10 \left( -\log_{10} \left(\frac{10^4\omega^4}{\omega_{\rm n}^4} \right) + \log_{10} \left(\frac{\omega^4}{\omega_{\rm n}^4} \right) \right) \\ &= -40\ {\rm [dB/dec]} \end{align}

零点を持つ場合

零点を持つ以下の二次遅れ系の伝達関数について考える。
G(s)=2ζωns+ωn2s2+2ζωns+ωn2\begin{align} G(s)=\frac{2\zeta\omega_{\rm n}s + \omega^2_{\rm n}}{s^2+2\zeta\omega_{\rm n}s + \omega^2_{\rm n}} \end{align}
ただし、ζ,ωn\zeta, \omega_{\rm n} は減衰率および固有角周波数とする。この伝達関数は次のように分解することができる。
G(s)=2ωns+2ωn+−2(1−ζ)ωns2+ωn2s(s+2ωn)(s2+2ζωns+ωn2)\begin{align} G(s)=\frac{2\omega_{\rm n}}{s+2\omega_{\rm n}} + \frac{-2(1-\zeta)\omega_{\rm n}s^2 + \omega^2_{\rm n}s}{(s+2\omega_{\rm n})(s^2+2\zeta\omega_{\rm n}s + \omega^2_{\rm n})} \end{align}
したがって、右辺第二項の影響が小さい場合には、零点を持つ二次遅れ系は二倍の固有角周波数を持つ一次遅れ系と類似した特性を示す。また、周波数伝達関数は次のように記述される。
G(jω)=ωn2+j2ζωnω(−ω2+ωn2)+j2ζωnω=ωn2ω4−2(1−2ζ2)ωn2ω2+ωn4ejϕ(ω)ϕ(ω)≡{tan⁡−1(2ζωωn)−tan⁡−1(2ζωnωωn2−ω2)(ω≠ωn)tan⁡−1(2ζωωn)−π2(ω=ωn)\begin{align} G(j\omega) &= \frac{\omega_{\rm n}^2 + j2\zeta\omega_{\rm n}\omega}{(-\omega^2 + \omega^2_{\rm n}) + j2\zeta\omega_{\rm n}\omega}\\ &= \frac{\omega^2_{\rm n}}{\sqrt{\omega^4 - 2(1-2\zeta^2)\omega^2_{\rm n}\omega^2 + \omega_{\rm n}^4}}e^{j\phi(\omega) } \\ \phi(\omega) &\equiv \left\{ \begin{matrix} \tan^{-1}\left( \frac{2\zeta\omega}{\omega_{\rm n}} \right) -\tan^{-1} \left(\frac{2\zeta\omega_{\rm n}\omega}{\omega^2_{\rm n} -\omega^2 }\right) & (\omega\neq\omega_{\rm n})\\ \tan^{-1}\left( \frac{2\zeta\omega}{\omega_{\rm n}} \right) -\frac{\pi}{2} & (\omega = \omega_{\rm n}) \end{matrix} \right. \end{align}
したがって、伝達関数の振幅特性は次式のように表され、ボード線図は下図のようになる。
g(ω)=10log⁡10(4ζ2ω2ωn2+1)−10log⁡10(1−2(1−2ζ2)ω2ωn2+ω4ωn4)\begin{align} g(\omega) &= 10 \log_{10} \left( 4\zeta^2\frac{\omega^2}{\omega_{\rm n}^2} + 1 \right) - 10 \log_{10} \left(1 - 2(1-2\zeta^2) \frac{\omega^2}{\omega_{\rm n}^2}+\frac{\omega^4}{\omega_{\rm n}^4} \right) \end{align}
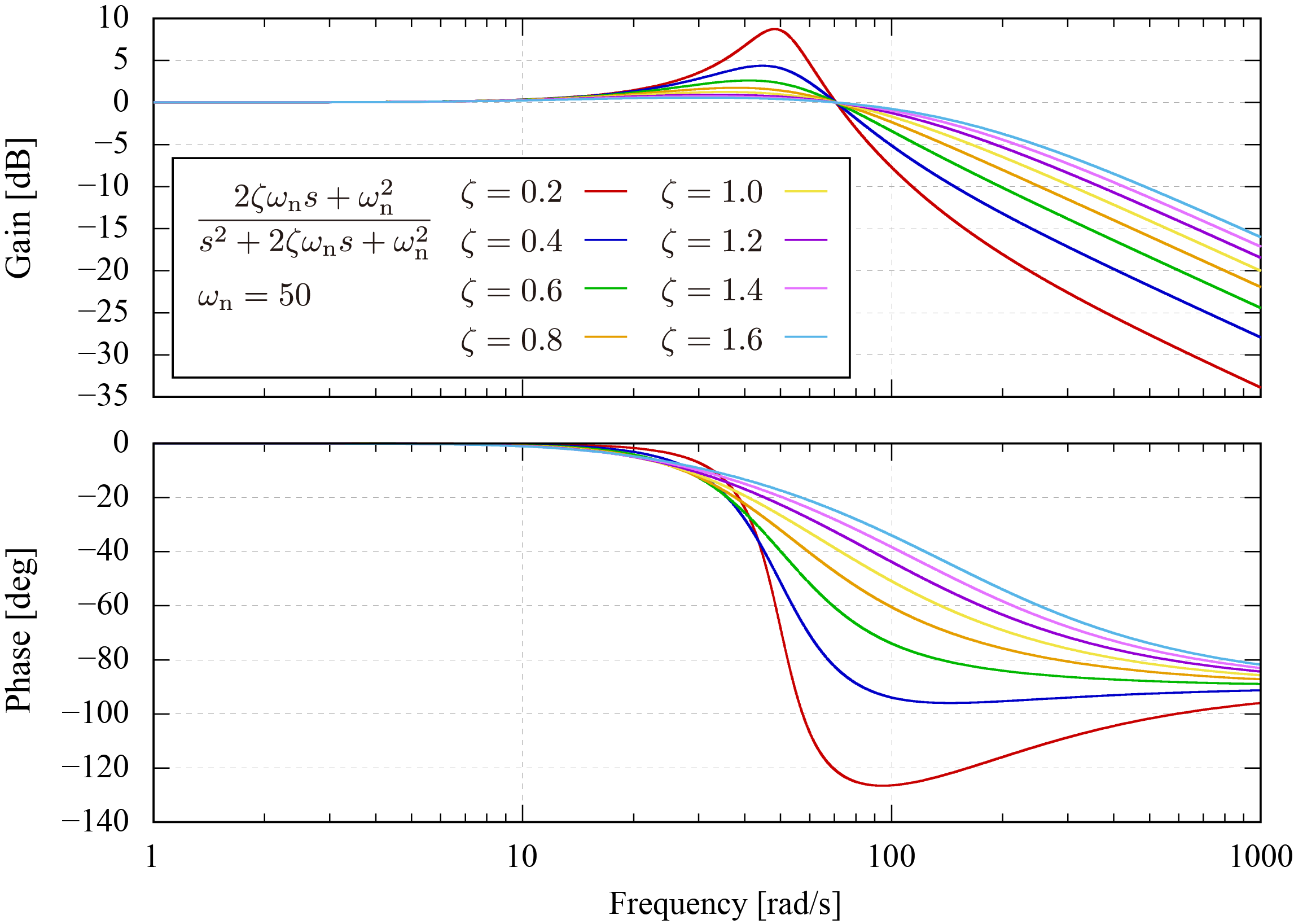
このモデルにおいて ωn=50\omega_{\rm n}=50 としたボード線図は下図のようになる。本図中では減衰率を 0.2∼1.60.2 \sim 1.6 の範囲で設定した場合の結果を示している。
image is here
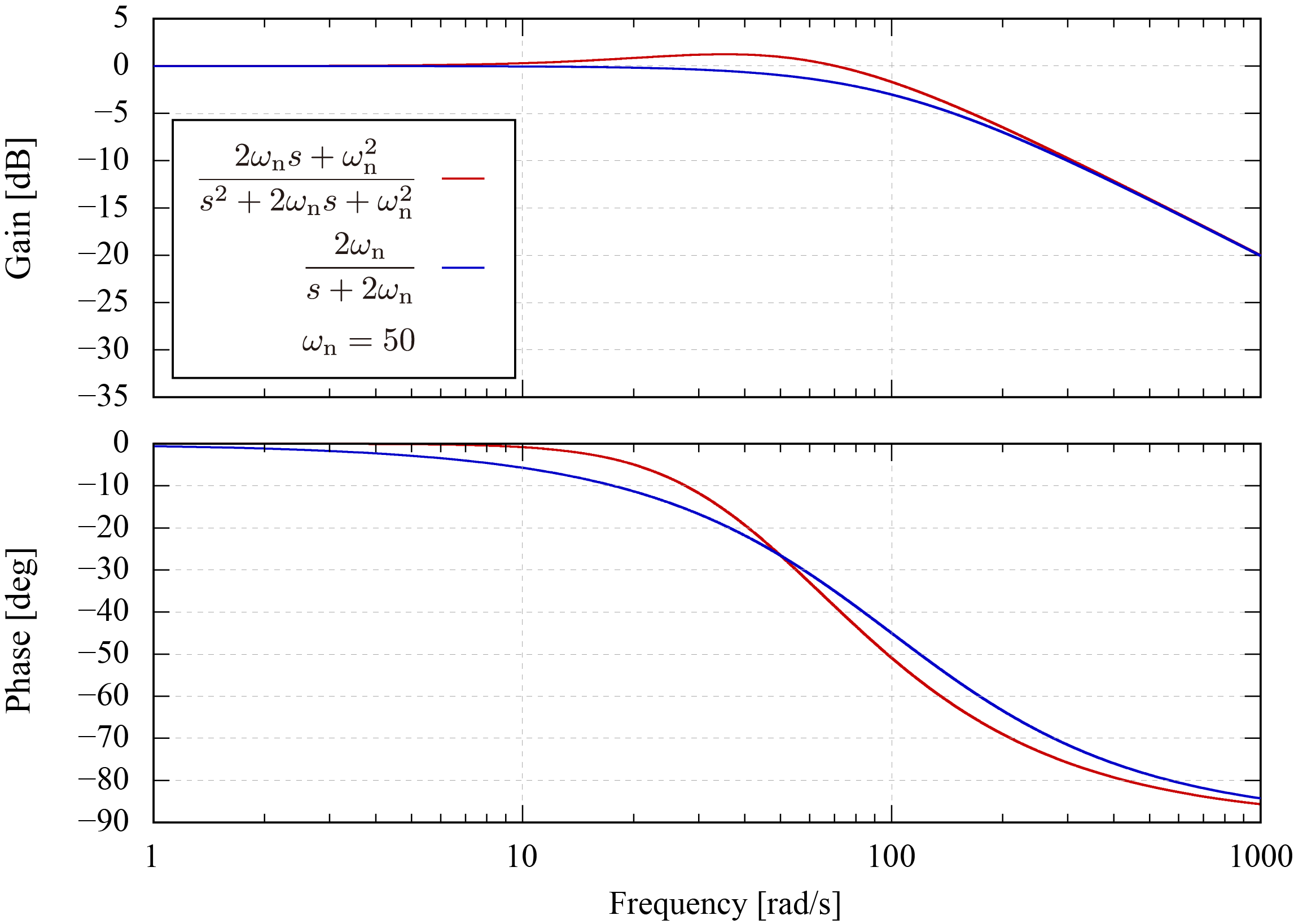
振幅特性が減少を開始する周波数を確認すると、固有角周波数の二倍の 100 rad/s100\ {\rm rad/s} 周辺であることが確認できる。また、減衰率 11 の場合の結果と二倍の固有角周波数を持つ一次遅れ系の結果を比較すると下図のようになる。
image is here
この図より、零点を持つ減衰率 11 の二次遅れ系は二倍の固有角周波数を持つ一次遅れ系と類似した周波数特性を示すことが確認できる。また、遮断帯域における振幅変化量は −20 [dB/dec]-20\ [{\rm dB/dec}] となる。

簡易安定性判別

ナイキストの安定判別法より、一巡伝達関数が不安定な極を持たない場合に閉ループが安定となる条件は、ナイキスト線図が点 (−1,j0)(-1, j0)を左に見て進むことと定義された。この条件を簡易的に確認するためには、一巡伝達関数の位相が −π-\pi を通過する際にゲインが 11 以下となることを確認すれば良い。ナイキスト線図は次数の高いシステムに対しても安定余裕度を確認しやすい利点があるが、不安定化の危険があり補償器を導入すべき周波数領域を特定することが難しい。ボード線図は厳密な安定判別を行うことは困難だが、安定余裕を確保すべき周波数帯域を特定しやすいといった利点がある。

安定余裕度の確認例

次の式で表現されるプラント PP の出力を制御することを考える。
P(s)=1s20.4s+120s+120e−0.01s\begin{align} P(s) = \frac{1}{s^2}\frac{0.4s + 120}{s+120}e^{-0.01s} \end{align}
この制御器に対して、以下のフィードバック制御器 CC を設置することを検討する。
C(s)=6s2+200s+1s2+200s×104\begin{align} C(s) = \frac{6s^2 + 200s + 1}{s^2 + 200s} \times 10^4 \end{align}
このとき、一巡伝達関数 LL は次のように表現される。
L(s)=PC=1s26s2+200s+1s2+200s0.4s+120s+120e−0.01s×104\begin{align} L(s) = PC =\frac{1}{s^2}\frac{6s^2 + 200s + 1}{s^2 + 200s}\frac{0.4s + 120}{s+120}e^{-0.01s} \times 10^4 \end{align}
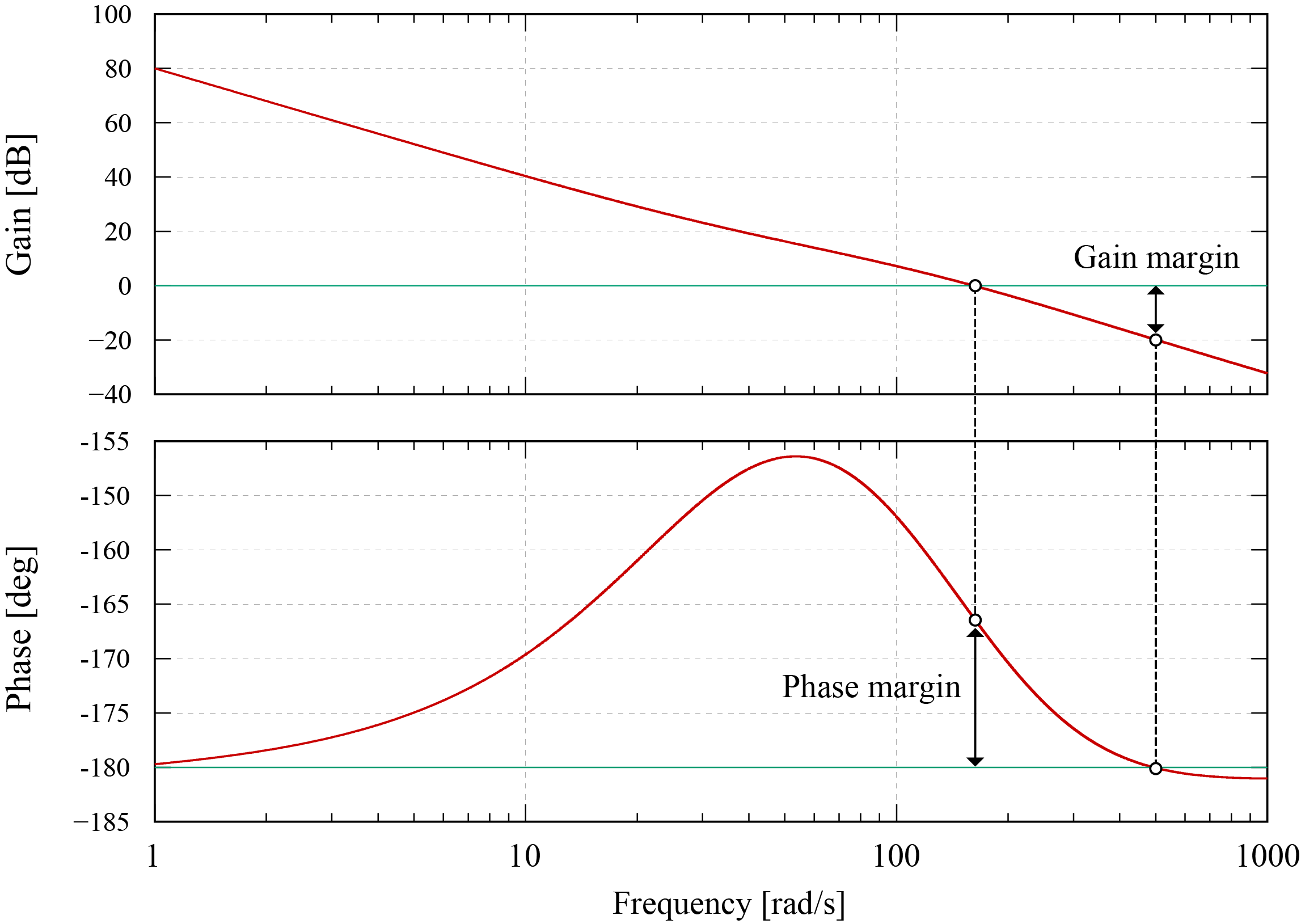
この一巡伝達関数のボード線図は下図のようになる。
image is here
この図において、振幅が 0dB0 {\rm dB} となる周波数をゲインクロスオーバ周波数 ωgc\omega_{\rm gc}、位相が −π-\pi となる周波数を位相クロスオーバ周波数 ωpc\omega_{\rm pc}と呼ぶ。また、振幅・位相に関する安定余裕度は次のように算出することができ、これらの値が 00 以上となれば閉ループ系は安定となる。
gsm=−20log⁡10∣L(jωpc)∣ϕsm=∠L(jωgc)+π\begin{align} g_{\rm sm} &= - 20\log_{\rm 10}|L(j\omega_{\rm pc})|\\ \phi_{\rm sm} &= \angle L(j\omega_{\rm gc}) + \pi \end{align}
上記の設計では安定余裕度が 00 以上となるため、閉ループ系は安定となる。

CONTENTS

© DigitalServo