DigitalServo

Blog

About

Library

    線形制御系設計

    線形システムの表現
    線形システムの特性解析
    制御器設計
    観測器設計

    モーションコントロール

    加速度制御
    剛体の姿勢制御

    モータドライブ

    駆動制御法
    磁極位置推定法

    システム同定

    ホワイトボックスモデル

二点吊り法による慣性同定

二点吊り法は系のホワイトボックスモデルを用いて測定対象の慣性を同定する手法である。ここでは系の運動モデルの導出およびこれに基づく慣性同定方法について述べる。

運動モデル

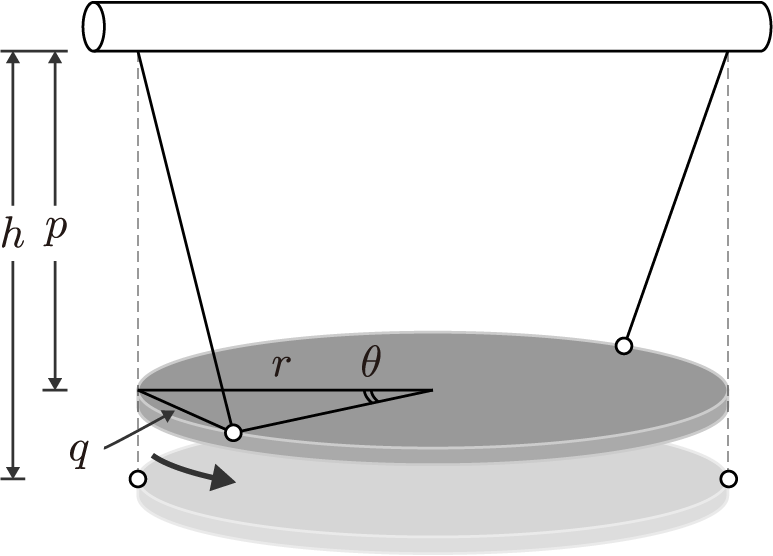
二点吊り法装置の構成を以下に示す。測定対象は二本の紐によって吊るされ，回転方向に自由度が与えられる。
image is here
ただし，h,r,θh, r, \theta はそれぞれ紐の長さ，回転中心から支点までの距離，回転角度を表し，p,qp, q は回転時の高さおよび弦長とする。このシステムの運動はラグランジュの運動方程式によって記述される。
ddt(∂L∂θ˙)−∂L∂θ=0\begin{align} \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta}} \right) - \frac{\partial L}{\partial \theta} = 0 \\ \end{align}
ただし，LL はラグランジアンを表し，運動エネルギ TT および ポテンシャルエネルギ UU によって次のように与えられる。
L=T−U\begin{align} L &= T-U \end{align}
ここで，運動エネルギ TT および ポテンシャルエネルギ UU は次のように記述される。
T=12Jθ˙2U=mg(h−p)\begin{align} T &= \frac{1}{2}J\dot{\theta}^2 \\ U &= mg\left(h - p\right) \end{align}
ただし，m,Jm, J は測定対象の質量および回転方向の慣性，gg は重力加速度を表す。ここで，装置の幾何学的関係よりポテンシャルエネルギ UU を次のように整理することができる。
q2=2r2(1−cos⁡θ)p=h2−q2=h2−2r2(1−cos⁡θ)∴U=mgh(1−1−2λ(1−cos⁡θ))λ≡r2h2\begin{align} q^2 &= 2r^2 (1 - \cos\theta) \\ p &= \sqrt{h^2 - q^2} \\ &= \sqrt{h^2 - 2r^2(1-\cos\theta)} \\ \therefore U &= mgh\left( 1 - \sqrt{1-2\lambda (1 - \cos\theta) }\right) \\ \lambda &\equiv \frac{r^2}{h^2} \end{align}
したがって，ラグランジアン LL は次のように表現される。
L=12Jθ˙2−mgh(1−1−2λ(1−cos⁡θ))\begin{align} L &= \frac{1}{2}J\dot{\theta}^2 - mgh\left( 1 - \sqrt{1-2\lambda (1 - \cos\theta) }\right) \end{align}
以上より，ラグランジュの運動方程式は次にように記述される。
Jθ¨+mghλsin⁡θ1−2λ(1−cos⁡θ)=0\begin{align} J\ddot{\theta} + mgh \frac{\lambda \sin\theta}{\sqrt{1-2\lambda (1 - \cos\theta)}} &= 0 \end{align}

慣性同定法

ラグランジュの運動方程式について，以下に示す関数 f(θ,λ)f(\theta, \lambda) を導入して整理する。
f(θ,λ)≡sin⁡θ1−2λ(1−cos⁡θ)→θ¨+mgr2Jhf(θ,λ)=0\begin{align} f(\theta, \lambda) &\equiv \frac{ \sin\theta}{ \sqrt{1-2\lambda (1 - \cos\theta)}} \\ \rightarrow \ddot{\theta} + & \frac{mgr^2}{Jh} f(\theta, \lambda) = 0 \\ \end{align}
ここで，線形近似 f(θ,λ)≈θf(\theta, \lambda) \approx \theta が成立する領域では支配方程式を次のように表現することができる。
θ¨+mgr2Jhθ=0\begin{align} \ddot{\theta} + \frac{mgr^2}{Jh} \theta&= 0 \\ \end{align}
この時，装置の回転方向の固有角周波数 ωn [rad/s]\omega_{\rm n}\ [{\rm rad/s}] は次のように記述される。
ωn=mgr2Jh\begin{align} \omega_{\rm n} &= \sqrt{\frac{mgr^2}{Jh}} \\ \end{align}
試験によって得られた共振周波数を fn [Hz]f_{\rm n}\ [{\rm Hz}] とすれば ωn=2πfn\omega_{\rm n}=2\pi f_{\rm n} が成立するため，慣性 JJ を次のように推定できる。
J^=mgr24π2fn2h\begin{align} \hat{J} &= \frac{mgr^2}{4\pi^2f_{\rm n}^2h} \end{align}

線形近似の適用可能性

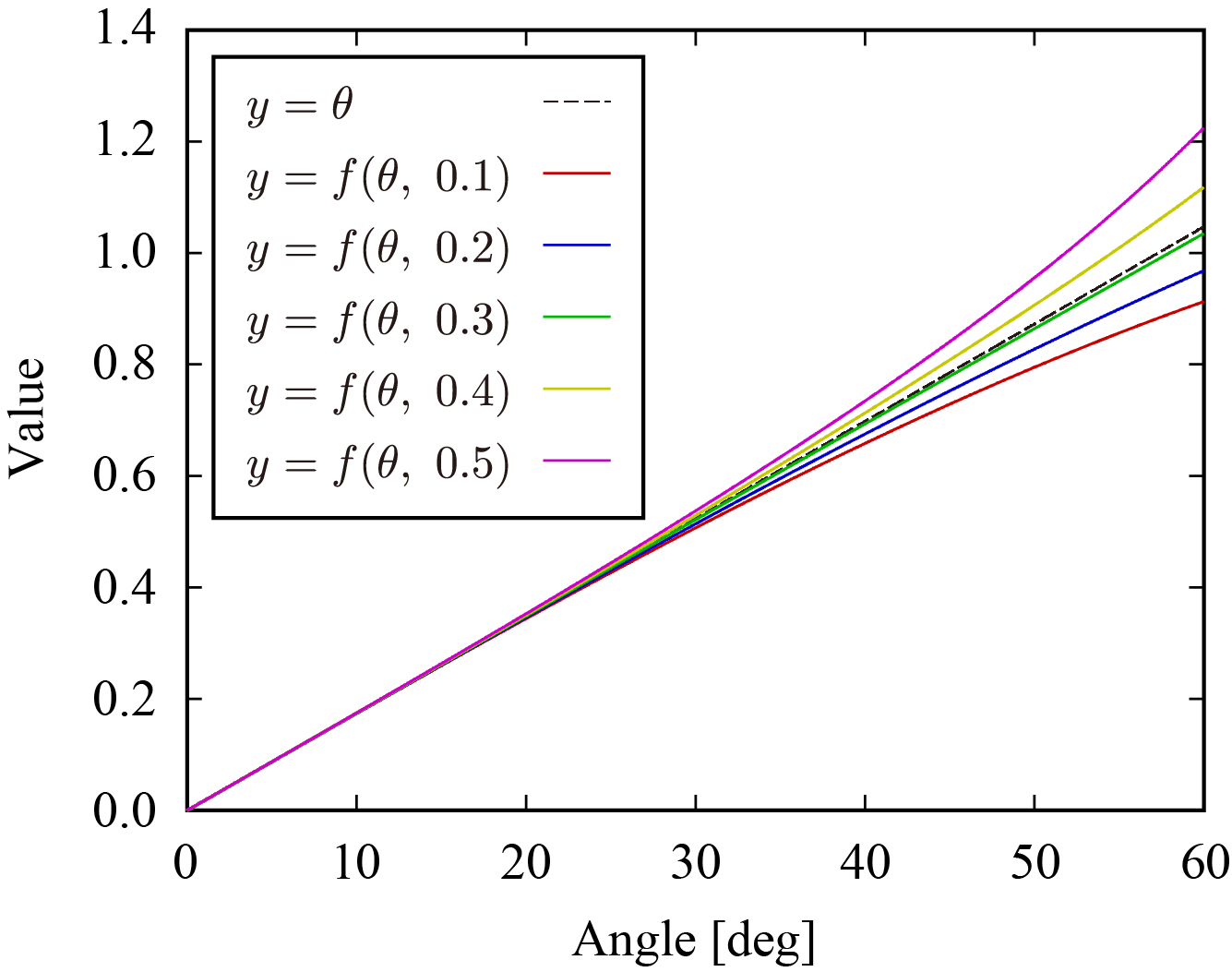
二点吊り法による慣性同定法が有効となるのは f(θ,λ)≈θf(\theta, \lambda) \approx \theta と見なせる場合である。関数 f(θ,λ)f(\theta, \lambda) は λ\lambda の関数であるため，同定精度は試験装置の構成に依存する。以下に λ\lambda を 0.1∼0.50.1\sim 0.5 の間で設定した関数 f(θ,λ)f(\theta, \lambda) を示す。ただし，関数 f(θ,λ)f(\theta, \lambda) は奇関数のため θ≥0\theta \ge 0 についてのみ図示した。
image is here
回転角度 θ\theta が十分に小さい場合には λ\lambda の値によらず f(θ,λ)≈θf(\theta, \lambda) \approx \theta と見ることができ，特に λ\lambda が 0.30.3 付近の値を取る場合に広い範囲で近似誤差が抑制されることが確認できる。近似誤差の差異は微小であるが，λ\lambda は同定精度を決定するパラメータとなる。ここで，線形近似誤差を最小化する λ\lambda について，次の損失関数 CC を最小化するものを解 λ∗\lambda^{\ast} とする。
C(θt,λ)=∫0θt(θ−f(θ,λ))2dθλ∗(θt)=arg min⁡λC(θt,λ)\begin{align} C(\theta_{\rm t}, \lambda) &= \int^{\theta_{\rm t}}_{0} \left( \theta - f(\theta, \lambda) \right)^2 d\theta \\ \lambda^{\ast}(\theta_{\rm t}) &= \argmin_{\lambda} C(\theta_{\rm t}, \lambda)\end{align}
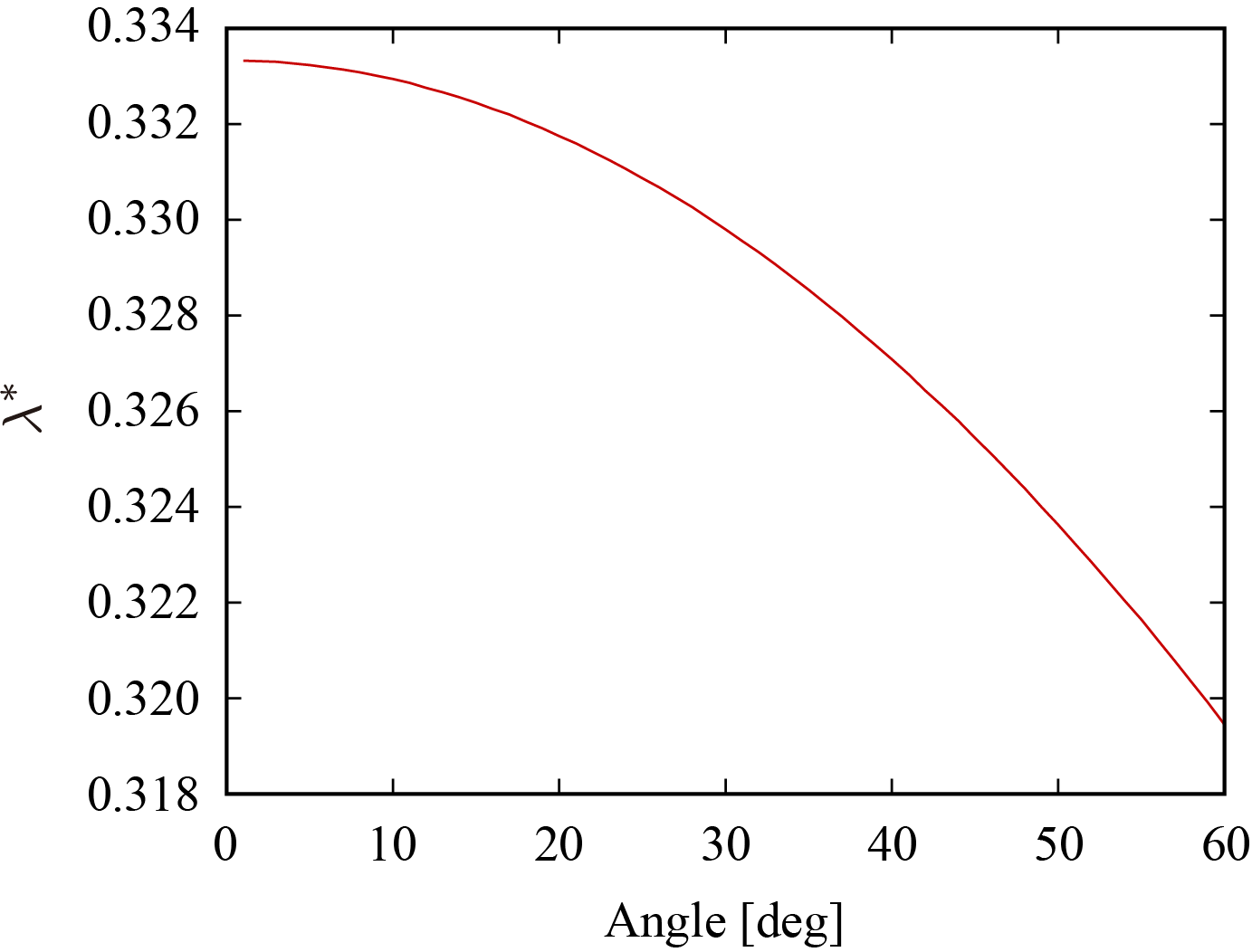
ただし，θt\theta_{\rm t} は積分区間を表すパラメータであり，試験にて使用する回転範囲とする。横軸を回転範囲 θt\theta_{\rm t} として，解 λ∗\lambda^{\ast} は数値計算によって次のように得られた。
image is here
以上より，λ\lambda として 0.330.33 付近の値を選ぶことで線形近似誤差を抑制することができる。この時，紐の長さ hh は回転中心から支点までの距離 rr によって次のように記述される。
h=rλ≈1.74r\begin{align} h &= \frac{r}{\sqrt{\lambda}} \approx 1.74r \end{align}
二点吊り法装置の構築においては，可能な限りこの関係を満たす設計を行うことが望ましい。

CONTENTS

© DigitalServo