カルマンフィルタ

問題定義

カルマンフィルタは確率統計の観点から状態推定を行う。ここでは以下のシステムについて考える。

\begin{align} \bm{x}[k+1]&=\bm{A}\bm{x}[k]+\bm{B}\bm{u}[k]+\bm{G}\bm{v} \\ \bm{\bm{y}}[k]&=\bm{C}\bm{x}[k]+\bm{w}, \end{align}

ただし，

\bm{x}

\bm{y},\bm{u}

は状態量，出力，入力を表し，

\bm{A}

\bm{B}

, and

\bm{C}

はシステム行列，入力行列，観測行列とする。また，

\bm{v}, \bm{w}

はそれぞれプロセス雑音と観測雑音とし，以下を満たすものとする。

\begin{align} {\rm E} \begin{bmatrix} \bm{v}\bm{v}^{\mathrm T} & \bm{w}\bm{v}^{\mathrm T} \\ \bm{v}\bm{w}^{\mathrm T} & \bm{w}\bm{w}^{\mathrm T} \end{bmatrix} = \begin{bmatrix} \bm{Q} & \bm{0} \\ \bm{0} & \bm{R} \end{bmatrix}. \end{align}

動作原理

フィルタ処理は予測ステップと修正ステップの2段階処理によって構成される。

予測ステップ

\begin{align} \bm{x}_{\rm p}[k+1]&=\bm{A}_{\rm m}\bm{x}_{\rm K}[k]+\bm{B}_{\rm m}\bm{u}[k] \\ \bm{y}_{\rm p}[k]&=\bm{C}_{\rm m}\bm{x}_{\rm p}[k], \end{align}

ただし，下添字

_{\rm m}

はモデルパラメータを示し,

_{\rm p}

および

_{\rm K}

は予測値と修正値であることを表す。

修正ステップ

\begin{align} \bm{x}_{\rm K}[k]&=\bm{x}_{\rm p}[k]+\bm{K}[k]\bm{e}_{\rm \bm{y}}[k] \\ \bm{e}_{\rm \bm{y}}[k] &\equiv \bm{\bm{y}}[k]-\bm{y}_{\rm p}, \end{align}

ここで，

\bm{K}

はカルマンゲインと呼ばれる。このゲインはシステムの事前情報，主にプロセス雑音や観測雑音の分散値によって一意に求まる。

カルマンゲインの導出

カルマンゲインは次の評価関数を最小化するように決定される。

\begin{align} J={\rm E}[|\bm{e}_{\rm \bm{y}}|]. \end{align}

このゲインは推定誤差共分散の時間発展を確認することで求めることができる。

予測誤差共分散の時間遷移

予測ステップにおける予測誤差は次のように表される。

\begin{align} \bm{x}[k+1]-\bm{x}_{\rm p}[k+1]&=\bm{A}\bm{x}[k]-\bm{A}_{\rm m}\bm{x}_{\rm K}[k]+\bm{B}\bm{u}[k]-\bm{B}_{\rm m}\bm{u}[k] +\bm{G}\bm{v} \\ &= \bm{A}(\bm{x}[k]-\bm{x}_{\rm p}[k])+\bm{G}\bm{v} \\ \therefore \bm{e}_{\rm p}[k+1]&=\bm{A}\bm{e}_{\rm K}[k]+\bm{G}\bm{v}. \\ (\bm{e}_{\rm p}[k]&\equiv \bm{x}[k]-\bm{x}_{\rm p}[k],\ \bm{e}_{\rm K}[k]\equiv \bm{x}[k]-\bm{x}_{\rm K}[k]) \end{align}

したがって，予測誤差共分散は次のように計算される。

\begin{align} \bm{e}_{\rm p}[k+1]\bm{e}_{\rm p}^{\mathrm T}[k+1]&=(\bm{A}\bm{e}_{\rm K}[k]+\bm{G}\bm{v})(\bm{A}\bm{e}_{\rm K}[k]+\bm{G}\bm{v})^{\mathrm T} \\ &=(\bm{A}\bm{e}_{\rm K}[k]+\bm{G}\bm{v})(\bm{e}_{\rm K}^{\rm T}[k]\bm{A}^{\mathrm T}+\bm{v}^{\mathrm T}\bm{G}^{\mathrm T}) \\ &= \bm{A}\bm{e}_{\rm K}[k]\bm{e}_{\rm K}^{\mathrm T}[k]\bm{A}^{\mathrm T}+\bm{A}\bm{e}_{\rm K}[k]\bm{v}^{\mathrm T}\bm{G}^{\mathrm T}+\bm{G}\bm{v}\bm{e}_{\rm K}^{\rm T}[k]\bm{A}^{\rm T}+\bm{G}\bm{v}\bm{v}^{\mathrm T}\bm{G}^{\mathrm T} \\ \therefore \bm{P}_{\rm p}[k+1]&=\bm{A}\bm{P}_{\rm K}[k]\bm{A}^{\mathrm T}+\bm{G}\bm{Q}\bm{G}^{\mathrm T}. \\ (\bm{P}_{\rm p}[k]&\equiv {\rm cov}\left[\bm{e}_{\rm p}[k]\right],\ \bm{P}_{\rm K}[k]\equiv{\rm cov}\left[\bm{e}_{\rm K}[k]\right]) \end{align}

推定誤差共分散の時間遷移

修正ステップにおける推定誤差は次にように表される。

\begin{align} \bm{e}_{\rm K}[k]&=\bm{x}[k]-\bm{x}_{\rm K}[k]\\&=\bm{x}[k]-(\bm{x}_{\rm p}[k]+\bm{K}[k]\bm{e}_{\rm \bm{y}}[k]) \\ &= \bm{x}[k]-\bm{x}_{\rm p}[k]-\bm{K}[k]\bm{\bm{y}}[k]+\bm{K}[k]\bm{C}_{\rm m}\bm{x}_{\rm p}[k] \\ &= \bm{x}[k]-\bm{x}_{\rm p}[k]-\bm{K}[k]\bm{C}\bm{x}[k]+\bm{K}[k]\bm{C}_{\rm m}\bm{x}_{\rm p}[k]+\bm{K}[k]\bm{w} \\ &= (\bm{I}-\bm{K}[k]\bm{C})\bm{e}_{\rm p}[k]+\bm{K}[k]\bm{w} \end{align}

したがって，推定誤差共分散は次のように計算される。

\begin{align} \bm{e}_{\rm K}[k]\bm{e}_{\rm K}^{\mathrm T}[k]=&\left((\bm{I}-\bm{K}[k]\bm{C})\bm{e}_{\rm p}[k]+\bm{K}[k]\bm{w}\right)\left((\bm{I}-\bm{K}[k]\bm{C})\bm{e}_{\rm p}[k]+\bm{K}[k]\bm{w}\right)^{\mathrm T} \\ =&\left((\bm{I}-\bm{K}[k]\bm{C})\bm{e}_{\rm p}[k]+\bm{K}[k]\bm{w}\right)\left(\bm{e}_{\rm p}^{\mathrm T}[k](\bm{I}-\bm{K}[k]\bm{C})^{\mathrm T}+\bm{w}^{\mathrm T}\bm{K}^{\mathrm T}[k]\right) \\ =&(\bm{I}-\bm{K}[k]\bm{C})\bm{e}_{\rm p}[k]\bm{e}_{\rm p}^{\mathrm T}[k](\bm{I}-\bm{K}[k]\bm{C})^{\mathrm T}+\bm{K}[k]\bm{w}\bm{w}^{\mathrm T}\bm{K}^{\mathrm T}[k]\\ &+\bm{K}[k]\bm{w} \bm{e}_{\rm p}^{\mathrm T}[k](\bm{I}-\bm{K}[k]\bm{C})^{\mathrm T}+(\bm{I}-\bm{K}[k]\bm{C})\bm{e}_{\rm p}[k]\bm{w}^{\mathrm T}\bm{K}^{\mathrm T}[k] \\ \therefore \bm{P}_{\rm K}[k]=& (\bm{I}-\bm{K}[k]\bm{C})\bm{P}_{\rm p}[k](\bm{I}-\bm{K}[k]\bm{C})^{\mathrm T}+\bm{K}[k]\bm{R}\bm{K}^{\mathrm T}[k] \\ =& \bm{P}_{\rm p}[k]- \bm{K}[k]\bm{C}\bm{P}_{\rm p}[k]-\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}\bm{K}^{\mathrm T}[k]+\bm{K}[k](\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})\bm{K}^{\mathrm T}[k]. \end{align}

カルマンゲイン

評価関数を最小化するために，フィルタシステムは以下を満たす必要がある。

\begin{align} \frac{\partial {\rm tr}(\bm{P}_{\rm K }[k])}{\partial \bm{K}[k]} &= -2(\bm{C}\bm{P}_{\rm p}[k])^{\mathrm T}+2\bm{K}[k](\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})=0. \end{align}

これにより，カルマンゲインは次のように決定される。

\begin{align} \bm{K}[k] &= \bm{P}_{\rm p}^{\mathrm T}[k] \bm{C}^{\mathrm T}(\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})^{-1} \\ &= \bm{P}_{\rm p}[k] \bm{C}^{\mathrm T}(\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})^{-1}. \\ &(\because \bm{P}_{\rm p}[k]=\bm{P}_{\rm p}^{\mathrm T}[k]) \end{align}

また，カルマンゲインが適切に設定された場合，予測ステップにおける推定誤差共分散

\bm{P}_{\rm K}

は次のように簡略化される。

\begin{align} \bm{P}_{\rm K}[k]&= \bm{P}_{\rm p}[k]- \bm{K}[k]\bm{C}\bm{P}_{\rm p}[k]-\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}\bm{K}^{\mathrm T}[k]+\bm{K}[k](\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})\bm{K}^{\mathrm T}[k] \\ &= \bm{P}_{\rm p}[k]- \bm{K}[k]\bm{C}\bm{P}_{\rm p}[k]-\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}\bm{K}^{\mathrm T}[k]+\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}\bm{K}^{\mathrm T}[k] \\ &= (\bm{I}-\bm{K}[k]\bm{C})\bm{P}_{\rm p}[k]. \end{align}

定常カルマンフィルタ

線形時不変系に対してカルマンフィルタを設計した場合，定常状態において予測誤差共分散が一定値に収束する。予測誤差共分散

\bm{P}_{\rm p}

は次のような時間発展をする。

\begin{align} \bm{P}_{\rm p}[k+1]&=\bm{A}\bm{P}_{\rm K}[k]\bm{A}^{\mathrm T}+\bm{G}\bm{Q}\bm{G}^{\mathrm T} \\ &=\bm{A}(\bm{I}-\bm{K}[k]\bm{C})\bm{P}_{\rm p}[k]\bm{A}^{\mathrm T}+\bm{G}\bm{Q}\bm{G}^{\mathrm T} \\ &=\bm{A}(\bm{I}-\bm{P}_{\rm p}[k] \bm{C}^{\mathrm T}(\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})^{-1}\bm{C})\bm{P}_{\rm p}[k]\bm{A}^{\mathrm T}+\bm{G}\bm{Q}\bm{G}^{\mathrm T} \\ &=\bm{A}(\bm{P}_{\rm p}[k]-\bm{P}_{\rm p}[k] \bm{C}^{\mathrm T}(\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})^{-1}\bm{C}\bm{P}_{\rm p}[k])\bm{A}^{\mathrm T}+\bm{G}\bm{Q}\bm{G}^{\mathrm T}. \end{align}

定常状態において予測誤差共分散が一定値に収束したものとし，その値を

\bm{P}^{\ast}_{\rm p}

とすれば以下の等式が成立する。

\begin{align} \bm{P}^{\ast}_{\rm p}=\bm{A}(\bm{P}^{\ast}_{\rm p}-\bm{P}^{\ast}_{\rm p} \bm{C}^{\mathrm T}(\bm{C}\bm{P}^{\ast}_{\rm p}\bm{C}^{\mathrm T}+\bm{R})^{-1}\bm{C}\bm{P}^{\ast}_{\rm p})\bm{A}^{\mathrm T}+\bm{G}\bm{Q}\bm{G}^{\mathrm T}. \end{align}

このときカルマンゲインも一定値

\bm{K}^{\ast}

に収束する。

\begin{align} \bm{K}^{\ast} &= \bm{P}^{\ast}_{\rm p}[k] \bm{C}^{\mathrm T}(\bm{C}\bm{P}^{\ast}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})^{-1}. \end{align}

このカルマンゲインを有するカルマンフィルタを定常カルマンフィルタと呼ぶ。この値はオフライン計算で導出可能である。

フィルタ特性

カルマンフィルタの出力は，予測された状態量

\bm{A}_{\rm m}\bm{x}_{\rm K}

とシステムの応答

A\bm{x}

の相補信号を使用して構成される。

\begin{align} \bm{x}_{\rm K}[k]&=\bm{x}_{\rm p}[k]+\bm{K}[k](\bm{\bm{y}}[k]-\bm{C}_{\rm m}\bm{x}_{\rm p}[k]) \\ &=(\bm{I}-\bm{K}[k]\bm{C}_{\rm m})\bm{x}_{\rm p}[k]+\bm{K}[k]\bm{C}\bm{x}[k]+\bm{K}[k]\bm{w} \\ &=(\bm{I}-\bm{K}[k]\bm{C})\bm{x}_{\rm p}[k]+ \bm{K}[k](\bm{C}-\bm{C}_{\rm m})\bm{x}_{\rm p} + \bm{K}[k]\bm{C}\bm{x}[k]+\bm{K}[k]\bm{w} \\ &=(\bm{I}-\bm{F}[k])(\bm{A}_{\rm m}\bm{x}_{\rm K}[k-1]+\bm{B}_{\rm m}\bm{u}[k-1])+\bm{F}[k](\bm{A}\bm{x}[k-1]+\bm{B}\bm{u}[k-1]+\bm{G}\bm{v})+\bm{K}[k]\bm{w} + \Delta \\ &=(\bm{I}-\bm{F}[k])\bm{A}_{\rm m}\bm{x}_{\rm K}[k-1]+\bm{F}[k](\bm{A}\bm{x}[k-1]+\bm{G}\bm{v})+\bm{B}_{\rm m}\bm{u}[k-1] +\bm{K}[k]\bm{w} +\Delta, \\ \end{align}

ただし，

\bm{F},\ \bm{\Delta}

は以下の定義する。

\begin{align} \bm{F}[k] & \equiv \bm{K}[k]\bm{C} = \bm{P}_{\rm p}[k] \bm{C}^{\mathrm T}(\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R})^{-1}\bm{C}\\ \Delta & \equiv \bm{K}[k](\bm{C}-\bm{C}_{\rm m})\bm{x}_{\rm p}. \end{align}

\bm{F}[k]

は相補フィルタの内分点を与え，この値は予測と観測の誤差共分散によって決定される。視認性のため，式を整理して以下を得る。

\begin{align} \bm{e}_{\rm \bm{y}}[k] &=\bm{\bm{y}}[k]-\bm{y}_{\rm p}[k] \\ &=\bm{C}\bm{x}[k]-\bm{C}_{\rm m}\bm{x}_{\rm p}[k] +\bm{w} \\ &=\bm{C}\bm{e}_{\rm p}[k]+\bm{w}\\ \Leftrightarrow \bm{e}_{\rm \bm{y}}[k]\bm{e}_{\rm \bm{y}}^{\mathrm T}[k]&= (\bm{C}\bm{e}_{\rm p}[k]+\bm{w})(\bm{C}\bm{e}_{\rm p}[k]+\bm{w})^{\mathrm T} \\ &= (\bm{C}\bm{e}_{\rm p}[k]+\bm{w})(\bm{e}_{\rm p}^{\mathrm T}[k]\bm{C}^{\mathrm T}+\bm{w}^{\mathrm T}) \\ &= \bm{C}\bm{e}_{\rm p}[k]\bm{e}_{\rm p}^{\mathrm T}[k]\bm{C}^{\mathrm T}+\bm{C}\bm{e}_{\rm p}[k]\bm{w}+\bm{w}\bm{e}_{\rm p}^{\mathrm T}[k]\bm{C}^{\mathrm T}+\bm{w}\bm{w}^{\mathrm T} \\ \Leftrightarrow \bm{P}_{\rm \bm{y}}[k]&=\bm{C}\bm{P}_{\rm p}[k]\bm{C}^{\mathrm T}+\bm{R}\\ \therefore \bm{F}[k] &= \bm{K}[k]\bm{C} = \bm{P}_{\rm p}[k] \bm{C}^{\mathrm T}\bm{P}_{\rm \bm{y}}^{-1}[k]\bm{C}. \end{align}

簡易的な動作解析

カルマンフィルタの予測ステップと修正ステップは以下のように記述される。

\begin{align} \bm{x}_{\rm p}[k+1]&=\bm{A}_{\rm m}\bm{x}_{\rm K}[k]+\bm{B}_{\rm m}\bm{u}[k] \\ \bm{x}_{\rm K}[k]&=\bm{x}_{\rm p}[k]+\bm{K}[k](\bm{\bm{y}}[k]-\bm{C}_{\rm m}\bm{x}_{\rm p}[k]) \end{align}

ここで，予測値

\bm{x}_{\rm p}

と修正値

\bm{x}_{\rm K}

について代数的に整理することで，以下を得る。

\begin{align} \bm{x}_{\rm p}[k+1]&=\bm{A}_{\rm m}\bm{x}_{\rm p}[k]+\bm{B}_{\rm m}\bm{u}[k]+\bm{A}_{\rm m}\bm{K}[k](\bm{\bm{y}}[k]-\bm{C}_{\rm m}\bm{x}_{\rm p}[k])\\ \bm{x}_{\rm K}[k]&=(\bm{I}-\bm{F}[k])\bm{x}_{\rm p}[k] + \bm{F}\bm{x}[k] + \bm{K}[k](\bm{C}-\bm{C}_{\rm m})\bm{x}_{\rm p} + \bm{K}[k]\bm{w}. \end{align}

すなわち，カルマンフィルタは可変ゲイン

K

を有するLuenbergerオブザーバと相補フィルタの組み合わせと見ることができる。

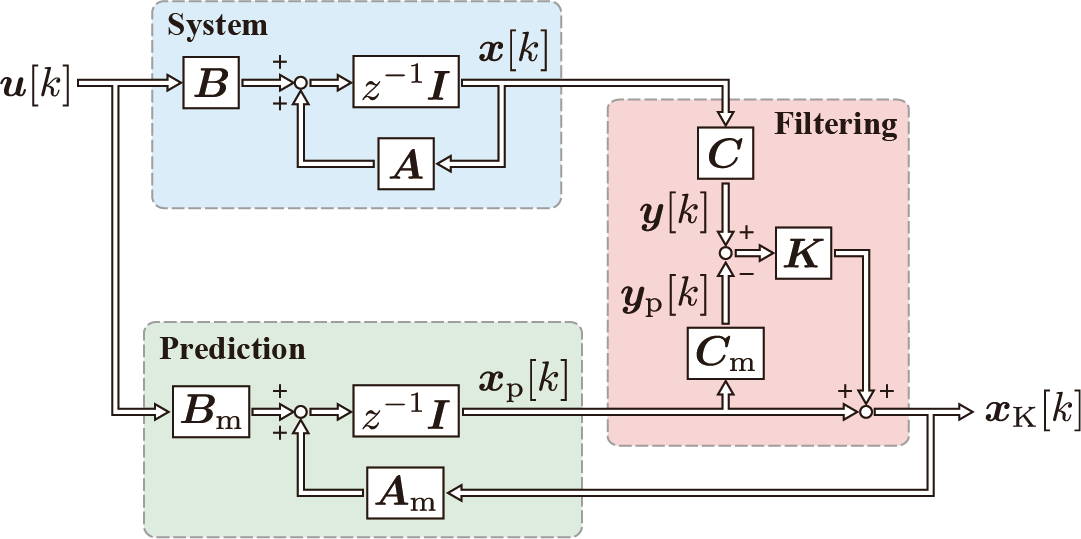
これはブロック線図からも確認することができる。予測ステップと修正ステップをブロック線図で示すと以下のようになる。簡潔のため，システムノイズについては省略している。

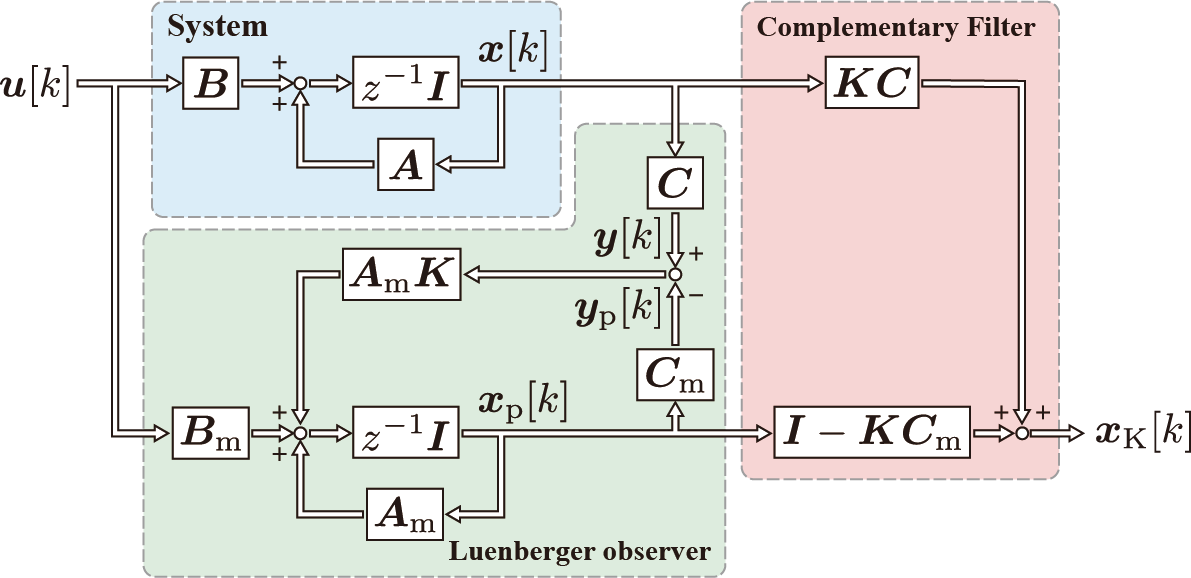
これを変形すれば以下のようになり，Luenbergerオブザーバと相補フィルタを確認することができる。

CONTENTS