DigitalServo

Blog

About

Library

    線形制御系設計

    線形システムの表現
    線形システムの特性解析
    制御器設計
    観測器設計

    モーションコントロール

    加速度制御
    剛体の姿勢制御

    モータドライブ

    駆動制御法
    磁極位置推定法

    システム同定

    ホワイトボックスモデル

同一次元オブザーバ

オブザーバはシステムの観測可能な状態から目的とする状態の推定を可能とする。このうち、状態空間表現における全ての状態を推定するものは同一次元オブザーバと呼ばれる。以下では同一次元オブザーバの構成方法について述べる。

設計方法

次の状態空間表現によって記述されるシステムについて考える。
x˙=Ax+Bu+vy=Cx+w\begin{align} \dot{\bm{x}}&=\bm{A}\bm{x}+\bm{B}\bm{u}+\bm{v} \\ \bm{y}&=\bm{C}\bm{x}+\bm{w} \end{align}
ただし、x,y,u\bm{x}, \bm{y}, \bm{u} は状態、出力、入力、A,B,C\bm{A}, \bm{B}, \bm{C} はシステム行列、入力行列、観測行列、v,w\bm{v}, \bm{w} はプロセス雑音と観測雑音を表す。この状態空間表現に対してシミュレーションモデルを作成し、並列に動作させることで状態の予測が可能となる。この予測は以下の状態空間モデルを用いて行われる。
x^˙=Anx^+Bnuy^=Cnx^\begin{align} \dot{\hat{\bm{x}}}&=\bm{A}_{\rm n}\hat{\bm{x}}+\bm{B}_{\rm n}\bm{u} \\ \hat{\bm{y}}&=\bm{C}_{\rm n}\hat{\bm{x}} \end{align}
ただし、下添字 n_{\rm n} は公称値、上添字 ^\hat{} は推定値を表す。この予測値にはモデル誤差やプロセス雑音の影響による誤差が含まれるため、これを補正するためにフィードバック機構を設ける。モデルを使用した予測に対し、オブザーバゲイン L\bm{L} を用いて次のように修正する。
x^˙=Anx^+Bnu+L(y−y^)y^=Cnx^\begin{align} \dot{\hat{\bm{x}}}&=\bm{A}_{\rm n}\hat{\bm{x}}+\bm{B}_{\rm n}\bm{u} + \bm{L}(\bm{y}-\hat{\bm{y}}) \\ \hat{\bm{y}}&=\bm{C}_{\rm n}\hat{\bm{x}} \end{align}
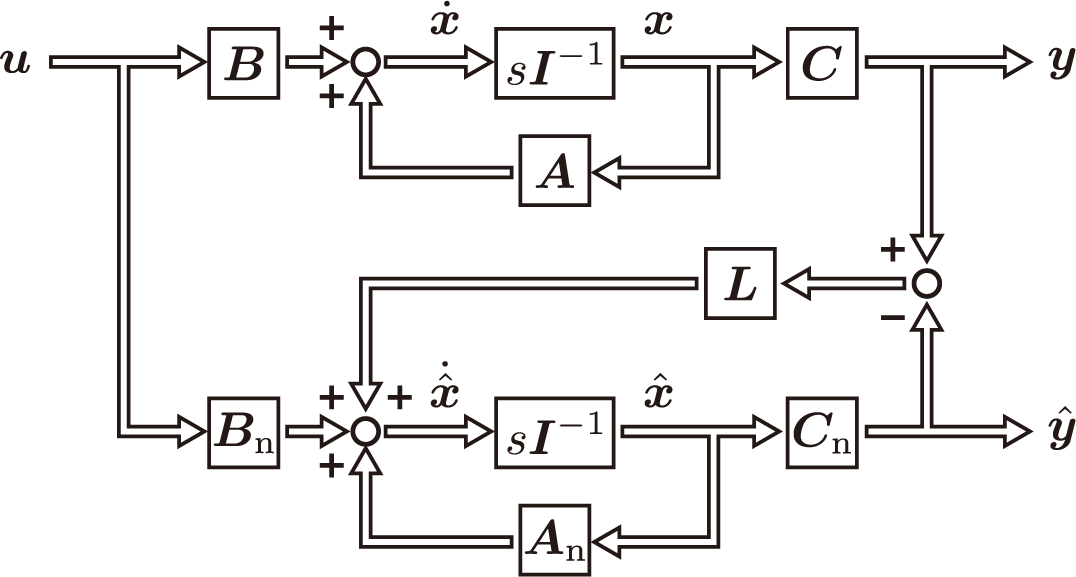
これにより状態空間表現における全状態量が推定される。このオブザーバは状態空間表現と同一数の状態を推定することから同一次元オブザーバ、またはLuenbergerのオブザーバと呼ばれる。同一次元オブザーバのブロック線図は以下のように表される。
image is here

誤差ダイナミクス

同一次元オブザーバによる推定について、推定誤差に関する以下の等式が成立する。
x˙−x^˙=(Ax+Bu+v)−(Anx^+Bnu+L(y−y^))=An(x−x^)+Aex+Beu−L(Cx+w−Cnx^)+v=An(x−x^)+Aex+Beu−LCn(x−x^)−LCex+v−Lw=(An−LCn)(x−x^)+(Ae−LCe)x+Beu+v−Lw\begin{align} \dot{\bm{x}}-\dot{\hat{\bm{x}}}&=\left(\bm{A}\bm{x}+\bm{B}\bm{u}+\bm{v}\right)-\left(\bm{A}_{\rm n}\hat{\bm{x}}+\bm{B}_{\rm n}\bm{u}+\bm{L}(\bm{y}-\hat{\bm{y}})\right) \\ &=\bm{A}_{\rm n}(\bm{x}-\hat{\bm{x}})+\bm{A}_{\rm e}\bm{x}+\bm{B}_{\rm e}\bm{u} -\bm{L}(\bm{C}\bm{x}+\bm{w}-\bm{C}_{\rm n}\hat{\bm{x}})+\bm{v} \\ &=\bm{A}_{\rm n}(\bm{x}-\hat{\bm{x}})+\bm{A}_{\rm e}\bm{x}+\bm{B}_{\rm e}\bm{u} -\bm{L}\bm{C}_{\rm n}(\bm{x}-\hat{\bm{x}})-\bm{L}\bm{C}_{\rm e}\bm{x}+\bm{v}-\bm{L}\bm{w} \\ &=(\bm{A}_{\rm n}-\bm{L}\bm{C}_{\rm n})(\bm{x}-\hat{\bm{x}})+(\bm{A}_{\rm e}-\bm{L}\bm{C}_{\rm e})\bm{x}+\bm{B}_{\rm e}\bm{u}+\bm{v}-\bm{L}\bm{w} \end{align}
ただし、下添字 e_{\rm e} は行列 X\bm{X} に対して真値と公称値の誤差を表すものとする。
Xe=X−Xn\begin{align} \bm{X}_{\rm e} &= \bm{X}-\bm{X}_{\rm n} \end{align}
ここで、推定誤差は次のダイナミクスを有することが確認できる。
e˙=(An−LCn)e+(Ae−LCe)x+Beu+v−Lwe≡x−x^\begin{align} \dot{\bm{e}}&=(\bm{A}_{\rm n}-\bm{L}\bm{C}_{\rm n})\bm{e}+(\bm{A}_{\rm e}-\bm{L}\bm{C}_{\rm e})\bm{x}+\bm{B}_{\rm e}\bm{u}+\bm{v}-\bm{L}\bm{w}\\ \bm{e} &\equiv \bm{x} -\hat{\bm{x}} \end{align}
モデル化誤差の影響が十分に小さいと仮定した場合、誤差システムの安定性は An−LCn\bm{A}_{\rm n}-\bm{L}\bm{C}_{\rm n} によって決定し、誤差システムが安定であれば推定誤差は 00 に漸近する。また、推定誤差の減衰速度は誤差システムの極に依存し、極配置設計によって推定の周波数特性を設定することができる。

分離定理

モデル誤差が十分に小さい場合に、オブザーバの極とフィードバック制御系の極が独立に設計可能であることを分離定理と呼ぶ。ここではオブザーバの推定値を用いて以下に示すフィードバック制御系を構築することを考える。
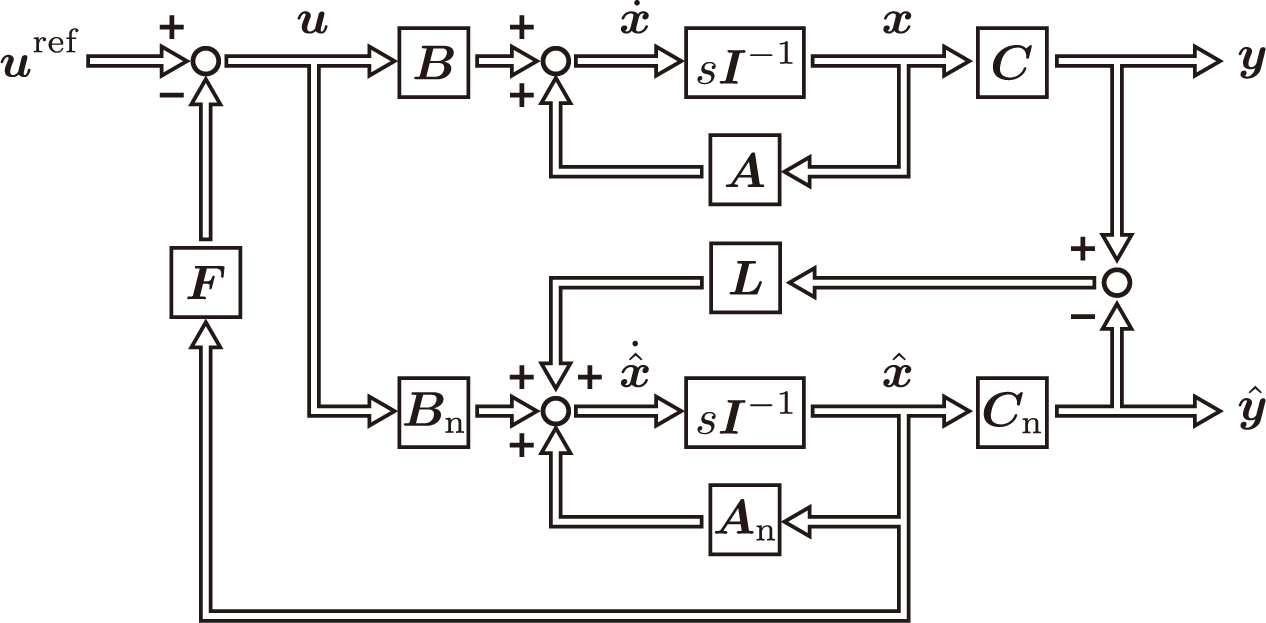
image is here
ただし、F\bm{F} はフィードバック制御器を表す。このシステムの概略図は以下のようになる。
image is here
オブザーバによる推定値のフィードバックは疑似的な状態フィードバックとなり、フィードバック制御系の極配置が可能となる。このとき，オブザーバの動作に関わらずフィードバック制御系の極は F\bm{F} によって決定され，またオブザーバの動作も F\bm{F} の影響を受けない。これが分離定理の主張であり，以下ではこの内容を確認する。上記のシステムについて，状態 x\bm{x} と推定誤差 e\bm{e} のダイナミクスは次のように表される。
x˙=Ax+B(uref−Fx^)+v=(A−BF)x+BFe+Buref+ve˙=(An−LCn)e+(Ae−LCe)x+Be(uref−Fx^)+v−Lw=(An−LCn+BeF)e+(Ae−LCe−BeF)x+Beuref+v−Lw\begin{align} \dot{\bm{x}}&=\bm{A}\bm{x}+\bm{B}(\bm{u}^{\rm ref}-\bm{F}\hat{\bm{x}})+\bm{v} \\ &=(\bm{A}-\bm{B}\bm{F})\bm{x}+\bm{B}\bm{F}e+\bm{B}\bm{u}^{\rm ref}+\bm{v} \\ \dot{\bm{e}}&=(\bm{A}_{\rm n}-\bm{L}\bm{C}_{\rm n})e+(\bm{A}_{\rm e}-\bm{L}\bm{C}_{\rm e})\bm{x}+\bm{B}_{\rm e}(\bm{u}^{\rm ref} - \bm{F}\hat{\bm{x}})+\bm{v}-\bm{L}\bm{w}\\ &=(\bm{A}_{\rm n}-\bm{L}\bm{C}_{\rm n}+\bm{B}_{\rm e}\bm{F})e+(\bm{A}_{\rm e}-\bm{L}\bm{C}_{\rm e}-\bm{B}_{\rm e}\bm{F})\bm{x}+\bm{B}_{\rm e}\bm{u}^{\rm ref}+\bm{v}-\bm{L}\bm{w} \end{align}
ここで、本来の状態空間表現の状態 x\bm{x} に推定誤差 e\bm{e} を追加した拡張状態空間表現について考える。
xE˙=AExE+BEuref+[II]v+[0−L]wxE≡[xe]AE≡[A−BFBFAe−LCe−BeFAn−LCn+BeF]BE≡[BBe]\begin{align} \dot{\bm{x}_{\rm E}} &= \bm{A}_{\rm E}\bm{x}_{\rm E} + \bm{B}_{\rm E} \bm{u}^{\rm ref} +\begin{bmatrix} \bm{I} \\ \bm{I} \end{bmatrix}\bm{v}+\begin{bmatrix} \bm{0} \\ -\bm{L} \end{bmatrix}\bm{w} \\ \bm{x}_{\rm E} &\equiv \begin{bmatrix} \bm{x} \\ \bm{e} \end{bmatrix}\\ \bm{A}_{\rm E} &\equiv \begin{bmatrix} \bm{A}-\bm{B}\bm{F} & \bm{B}\bm{F} \\ \bm{A}_{\rm e}-\bm{L}\bm{C}_{\rm e} -\bm{B}_{\rm e}\bm{F} & \bm{A}_{\rm n}-\bm{L}\bm{C}_{\rm n}+\bm{B}_{\rm e}\bm{F} \end{bmatrix}\\ \bm{B}_{\rm E} &\equiv \begin{bmatrix} \bm{B} \\ \bm{B}_{\rm e} \end{bmatrix} \end{align}
この表現において、モデル誤差が十分に小さい場合にシステム行列 AE\bm{A}_{\rm E} を次のように記述することができる。
AE≈[A−BFBF0An−LCn]\begin{align} \bm{A}_{\rm E} &\approx \begin{bmatrix} \bm{A}-\bm{B}\bm{F} & \bm{B}\bm{F} \\ \bm{0} & \bm{A}_{\rm n}-\bm{L}\bm{C}_{\rm n}\end{bmatrix} \end{align}
したがって，制御システムおよびオブザーバの極配置はそれぞれフィードバック制御器 F\bm{F} およびオブザーバゲイン L\bm{L} によって独立に設計可能である。

CONTENTS

© DigitalServo