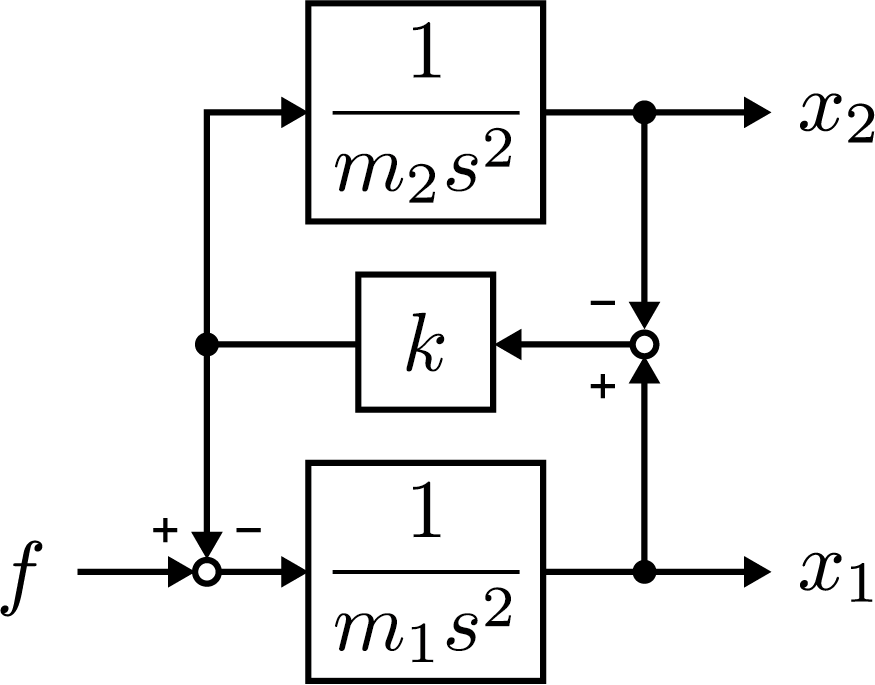ブロック線図は信号の流れを視覚的に確認するために使用される。

入力 $r$ から出力 $y$ までの伝達関数が $G$ と表現される場合、次のように表現する。

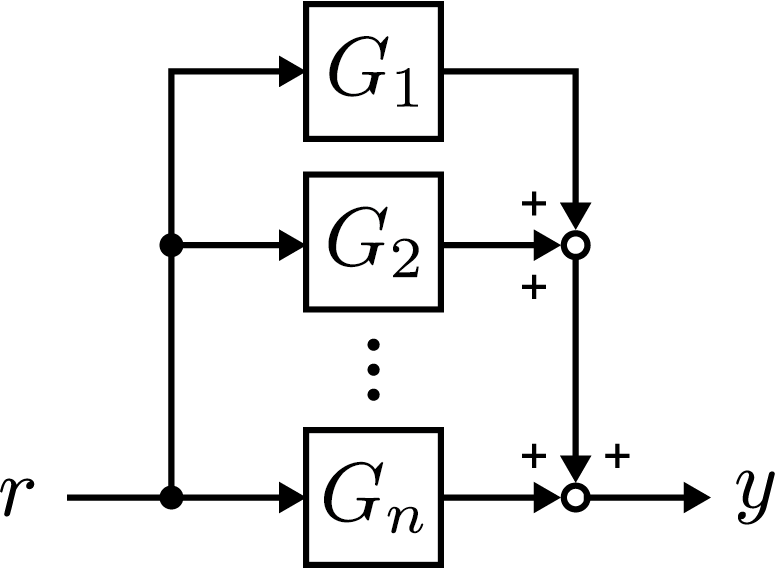
システム全体を表現する場合には複数のブロックを接続することで表現する。 そのような場合にはシステムの線形性等を利用してブロック線図を等価変換し、視認性の高い表現に変形することができる。

システムが線形であるとき、線形写像の和および合成も線形写像となることから、並列接続されたブロックの伝達関数は次のようになる。

また、直列接続されたブロックの伝達関数は次のようになる。

線形写像の合成は可換であるため、直列接続されたブロックの順序を入れ替えた場合にも入出力伝達関数は変化しない。

入出力の開ループ伝達特性が $G_{\rm op}(s)$, 帰還伝達特性が $H(s)$の伝達経路から構成されるフィードバック系について考える。

この入出力特性は、次の代数方程式を解くことで得られる。

伝達関数の積 $GH$ は経路を一巡し帰還するまでの伝達特性を表し、一巡伝達関数と呼ばれる。フィードバック制御系の閉ループ伝達関数 $G_{cl}$ は、開ループ伝達特性伝達特性 $G_{\rm op}$、一巡伝達特性 $L$ を用いて次のように記述される。

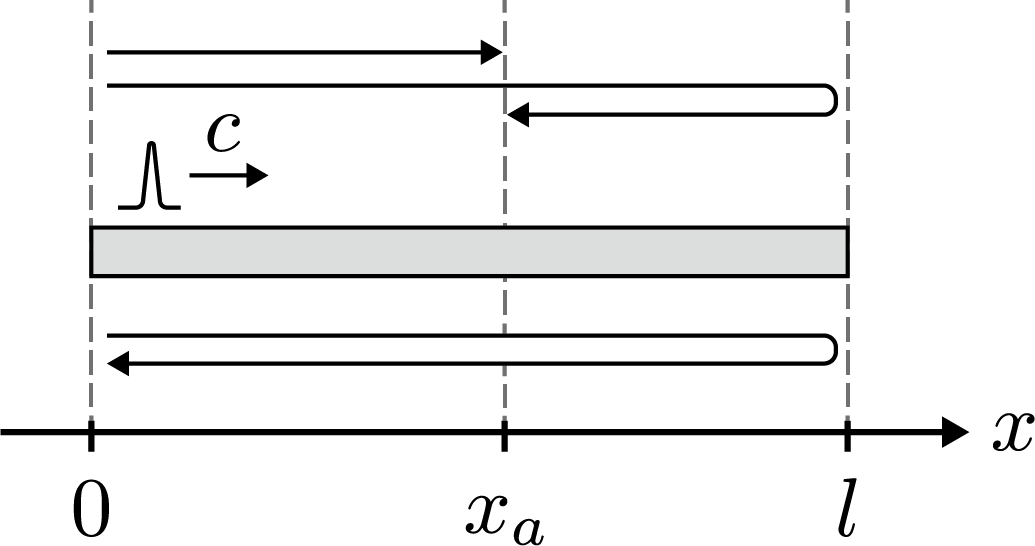
フィードバックシステムにおける開ループ伝達と一巡伝達の作用を理解するために、一次元波動方程式で表現される波動現象について確認する。波動現象は波の伝達によって記述することが可能であり、波の進行と反射からなるフィードバック系として説明することができる。ここでは有界領域 $x \in [0, l]$ において定義される以下の一次元波動方程式について考える。ただし、$t, x, c$ はそれぞれ時刻、座標、波速を表し、$y(x,t)$は時刻 $t$、座標 $x$ における波の変位を表す。

このシステムの期状態は以下のように記述されるものとする。

このシステムの始点は強制変位 $u(t)$ で与えられ、また終点は自由端であるとして境界条件を以下のように記述する。

この条件下で偏微分方程式を解くことにより、次の解を得る。

ここで、任意の座標$y(x, s)$ は $y(x, t)$ のラプラス変換を表す。始点の変位 $u(t)$ から座標 $x$ の変位 $y(x, t)$ までの伝達関数は時間遅れ要素を用いて表現される。この遅れは波の伝播の遅れと見ることができる。伝達関数の分子に存在する二つの時間遅れ要素は、始点から発生した波が座標 $x$ に到達するまでの時間 $x/c$ と、終点で反射した後に座標 $x$ に到達するまでの時間 $(2l - x)/c$ を表す。すなわち、分子は始点から発生した波の座標 $x$ における進行波と反射波の和となり、開ループ伝達特性を表すことがわかる。また、伝達関数の分母に存在する時間遅れ要素は始点から発生した波の往復時間 $2l/c$ と一致し、一巡伝達関数であることが確認できる。

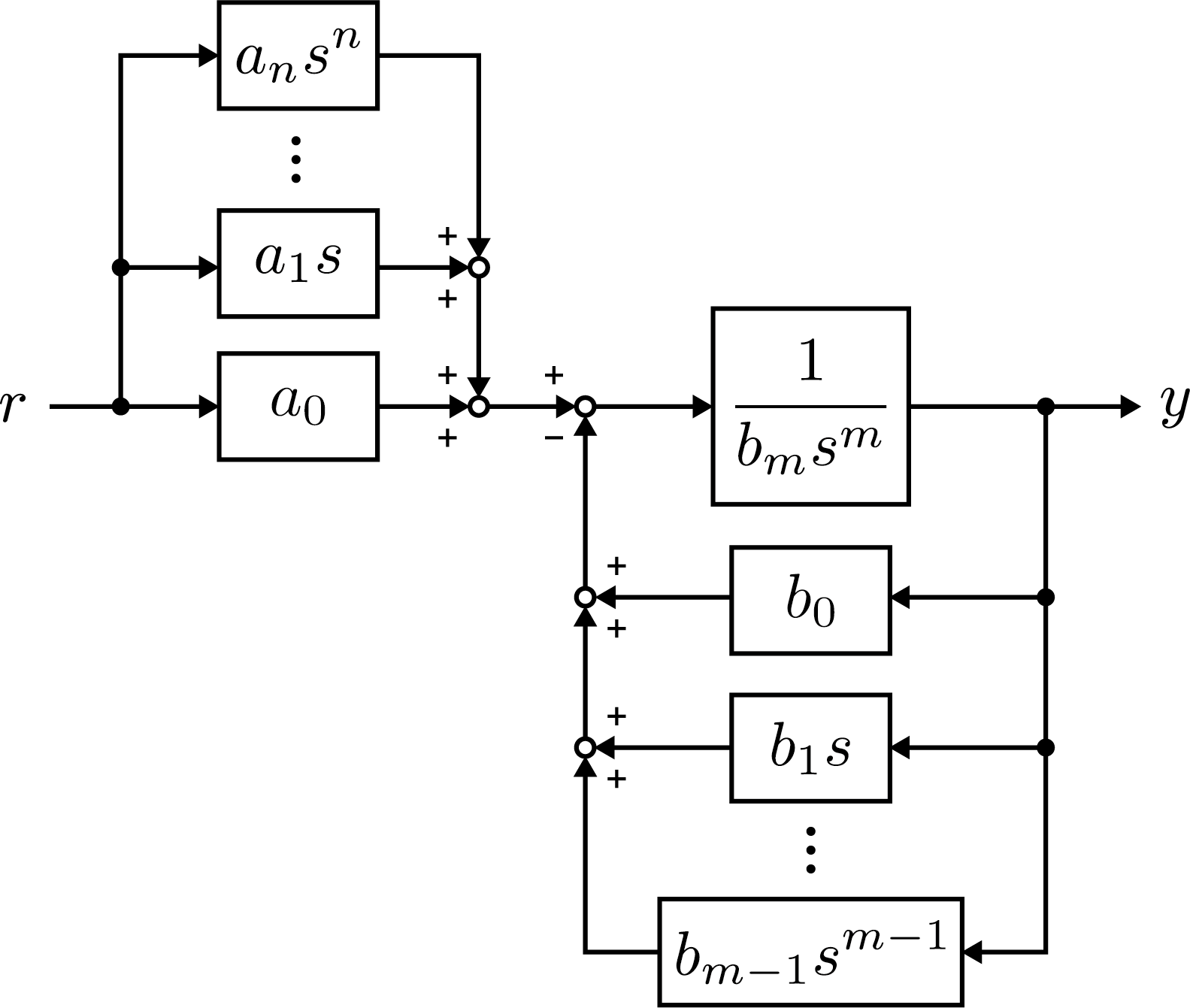
実数 $a_{i}\ (i=1,...,n)$ および $b_{j}\ (j=1,...,m)$ により伝達関数 $G$ が次のように表現される場合について考える。ただし、$n \le m$ とする。

この伝達関数に関して次のように変形する。

ここで、次のブロック線図は上記の伝達特性を実現するものとなる。

ブロック線図は微分方程式で記述されるシステムに対する視認性を向上し、システムの特性に対する理解を補助することができる。 高次のダイナミクスを持つシステムは複雑な入出力伝達関数を有するが、微分方程式からブロック線図を構築することで物理的に明快な表現を与える。 また、この表現ではシステム内部の信号の流れが確認できることから、物理的知見からの設計を促進する。

振動現象を記述するモデルとして、多慣性共振系が挙げられる。ここでは簡単のため二慣性共振系の伝達関数を計算することを目的とし、以下の連立微分方程式で記述されるシステムを考える。ただし、$m_{1}, m_{2}$ および $x_{1}, x_{2}$ は慣性体 $1, 2$ の質量および座標とし、$k, f$ は復元力定数および慣性体 $1$ に作用する外力とする。

この連立微分方程式からブロック線図を作成すると、次の表現を得る。

ここで、ブロック線図より次の関係式を見つけることができる。