制御対象のモデルと実プラントの動作には差異があるという認識の下、制御系がこの不確かさに対して安定性と制御性能を確保するとき、制御系はロバストであるという。プラントの不確かさに対して安定性を保持することをロバスト安定、さらに性能目標が満たされることを指してロバスト性能と呼ぶ。
モデルの不確かさは、モデル化が困難な現象(局所的非線形性や温湿度等に対する外環境依存性、高次ダイナミクスなど)に起因して生じる誤差、製造過程におけるばらつき、経年劣化による物理特性の変化などが挙げられる。制御器はこれらの不確かさを許容する必要があり、解析的な設計を行うためには不確かさのモデルを導入する必要がある。不確かさを表現するモデルとしては加法的誤差および乗法的誤差が使用される。ただし、
P , P n \bm{P}, \bm{P}_{\rm n} P , P n はそれぞれ実プラントおよびノミナルモデルを表し、
Δ P \bm{\Delta}_{\rm P} Δ P は不確かさを表すものとする。
P = P n + Δ P \begin{align}
\bm{P} = \bm{P}_{\rm n} + \bm{\Delta}_{\bm{P}}
\end{align} P = P n + Δ P P = ( I + Δ P ) P n \begin{align}
\bm{P} = (\bm{I} + \bm{\Delta}_{\bm{P}})\bm{P}_{\rm n}
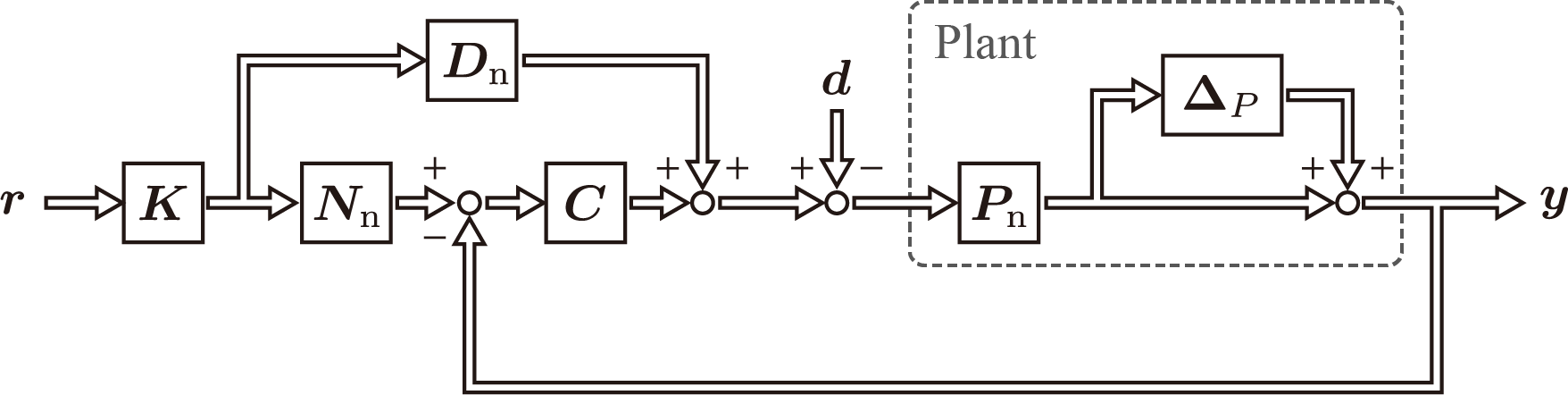
\end{align} P = ( I + Δ P ) P n モデルの不確かさが二自由度制御系に与える影響について考える。不確かさは乗法的誤差として記述する。プラントのノミナルモデルの右既約分解表現を
P n = N n D n − 1 \bm{P}_{\rm n} = \bm{N}_{\rm n}\bm{D}_{\rm n}^{-1} P n = N n D n − 1 として,二自由度制御系は次のように表される。
この制御系の出力
y \bm{y} y は次のように記述される。
y = ( I + P C ) − 1 ( P P n − 1 + P C ) N n K r − ( I + P C ) − 1 P d \begin{align}
\bm{y} &= (\bm{I} + \bm{P}\bm{C})^{-1}( \bm{P}\bm{P}_{\rm n}^{-1} + \bm{P}\bm{C} ) \bm{N}_{\rm n}\bm{K}\bm{r} - (\bm{I} + \bm{P}\bm{C})^{-1}\bm{P}\bm{d} \\
\end{align} y = ( I + P C ) − 1 ( P P n − 1 + P C ) N n K r − ( I + P C ) − 1 P d ここで、実プラントの特性が
P \bm{P} P と表される場合の指令値伝達関数と外乱伝達特性をそれぞれ
T r y ( P ) , T d y ( P ) \bm{T}_{\bm{ry}}(\bm{P}), \bm{T}_{\bm{dy}}(\bm{P}) T ry ( P ) , T dy ( P ) として出力を表現する。
y = T r y ( P ) r − T d y ( P ) d T r y ( P ) ≡ ( I + P C ) − 1 P ( P n − 1 + C ) N n K T d y ( P ) ≡ ( I + P C ) − 1 P \begin{align}
\bm{y}&= \bm{T}_{\bm{ry}}(\bm{P}) \bm{r} - \bm{T}_{\bm{dy}}(\bm{P})\bm{d} \\
\bm{T}_{\bm{ry}}(\bm{P}) &\equiv (\bm{I} + \bm{P}\bm{C})^{-1} \bm{P}(\bm{P}_{\rm n}^{-1} + \bm{C} ) \bm{N}_{\rm n}\bm{K}\\
\bm{T}_{\bm{dy}}(\bm{P}) &\equiv (\bm{I} + \bm{P}\bm{C})^{-1}\bm{P}
\end{align} y T ry ( P ) T dy ( P ) = T ry ( P ) r − T dy ( P ) d ≡ ( I + P C ) − 1 P ( P n − 1 + C ) N n K ≡ ( I + P C ) − 1 P このシステムについて
P = P n \bm{P}=\bm{P}_{\rm n} P = P n 、即ち
Δ P = 0 \bm{\Delta}_{\bm{P}}=\bm{0} Δ P = 0 における性能および安定性をノミナル性能およびノミナル安定性と呼ぶ。また、実プラント
P \bm{P} P がノミナルモデル
P n \bm{P}_{\rm n} P n から変動した場合について,プラントの変動率
R P \bm{R}_{\bm{P}} R P と指令値追従性能の変動率
R T \bm{R}_{\bm{T}} R T は次のように記述される。
R P = ( P − P n ) P − 1 = I − P n P − 1 R T = ( T r y ( P ) − T r y ( P n ) ) T r y − 1 ( P ) = I − T r y ( P n ) T r y − 1 ( P ) = ( I + P n C ) − 1 ( I − P n P − 1 ) ∴ R T = ( I + P n C ) − 1 R P \begin{align}
\bm{R}_{\bm{P}} &= (\bm{P} - \bm{P}_{\rm n}) \bm{P}^{-1} \\
&= \bm{I} - \bm{P}_{\rm n}\bm{P}^{-1} \\
\bm{R}_{\bm{T}} &= \left(\bm{T}_{\bm{ry}}(\bm{P}) - \bm{T}_{\bm{ry}}(\bm{P}_{\rm n}) \right) \bm{T}_{\bm{ry}}^{-1}(\bm{P}) \\
&= \bm{I} - \bm{T}_{\bm{ry}}(\bm{P}_{\rm n}) \bm{T}_{\bm{ry}}^{-1}(\bm{P}) \\
&= (\bm{I} + \bm{P}_{\rm n}\bm{C})^{-1}(\bm{I} - \bm{P}_{\rm n}\bm{P}^{-1})\\
\therefore \bm{R}_{\bm{T}} &= (\bm{I} + \bm{P}_{\rm n}\bm{C})^{-1}\bm{R}_{\bm{P}}
\end{align} R P R T ∴ R T = ( P − P n ) P − 1 = I − P n P − 1 = ( T ry ( P ) − T ry ( P n ) ) T ry − 1 ( P ) = I − T ry ( P n ) T ry − 1 ( P ) = ( I + P n C ) − 1 ( I − P n P − 1 ) = ( I + P n C ) − 1 R P この式はプラントの変動率に対する指令値追従性能の変動率の感度特性を表し、その特性は感度関数
S \bm{S} S によって示される。また、感度関数に相補的な関数
I − S \bm{I}-\bm{S} I − S を相補感度関数
T \bm{T} T と呼び、これら二つの関数によって制御性能を評価することができる。
S = ( I + P n C ) − 1 T = ( I + P n C ) − 1 P n C \begin{align}
\bm{S} &= (\bm{I} + \bm{P}_{\rm n}\bm{C})^{-1} \\
\bm{T} &= (\bm{I} + \bm{P}_{\rm n}\bm{C})^{-1}\bm{P}_{\rm n}\bm{C} \\
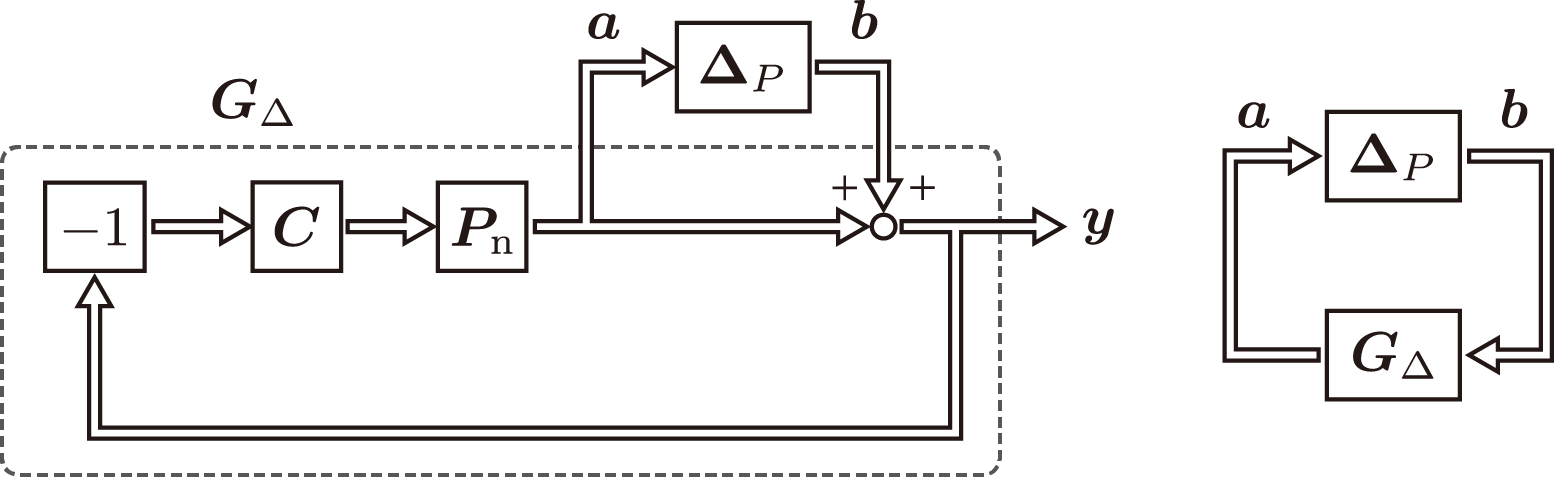
\end{align} S T = ( I + P n C ) − 1 = ( I + P n C ) − 1 P n C システムがノミナル安定であり、プラントの不確かさによってシステムが不安定化しなければロバスト安定となる。この安定性について、不確かさを含む一巡伝達関数を確認することで判別することができる。プラントの不確かさを起点としてブロック線図を見た場合、次のように表現することができる。
ここで、
G Δ \bm{G}_{\Delta} G Δ は信号
b \bm{b} b から
a \bm{a} a までの伝達特性を表す。この伝達関数は次のように表される。
a = − P n C ( a + b ) ∴ G Δ = − ( I + P n C ) − 1 P n C \begin{align}
\bm{a} &= -\bm{P}_{\rm n}\bm{C}(\bm{a} + \bm{b}) \\
\therefore \bm{G}_{\Delta} &= -(\bm{I} + \bm{P}_{\rm n}\bm{C})^{-1} \bm{P}_{\rm n}\bm{C}
\end{align} a ∴ G Δ = − P n C ( a + b ) = − ( I + P n C ) − 1 P n C したがって,不確かさを含むフィードバック系の一巡伝達関数
L \bm{L} L は以下のように表される。
L = G Δ Δ P = − T Δ P \begin{align}
\bm{L} &= \bm{G}_{\Delta} \bm{\Delta}_{\bm{P}} = -\bm{T}\bm{\Delta}_{\bm{P}}
\end{align} L = G Δ Δ P = − T Δ P 以上より,ロバスト安定となる条件はスモールゲイン定理より次のように記述される。
∥ T Δ P ∥ ∞ < 1 \begin{align}
\| \bm{T}\bm{\Delta}_{\bm{P}} \|_{\infty} < 1
\end{align} ∥ T Δ P ∥ ∞ < 1 ここで、
∥ ⋅ ∥ ∞ \|\cdot\|_{\infty} ∥ ⋅ ∥ ∞ は
H ∞ H_{\infty} H ∞ ノルムを表す。
伝達関数
G ( s ) G(s) G ( s ) の
H ∞ H_{\infty} H ∞ ノルムは以下の値をとる。
∥ G ( s ) ∥ ∞ = sup ω ∣ G ( j ω ) ∣ \begin{align}
\|G(s)\|_{\infty} = \sup_{\omega}\ |G(j\omega)|
\end{align} ∥ G ( s ) ∥ ∞ = ω sup ∣ G ( jω ) ∣ また、伝達関数行列
G ( s ) \bm{G}(s) G ( s ) の
H ∞ H_{\infty} H ∞ ノルムは以下の値をとる。
∥ G ( s ) ∥ ∞ = sup ω σ { G ( j ω ) } \begin{align}
\|\bm{G}(s)\|_{\infty} = \sup_{\omega}\ \sigma\{\bm{G}(j\omega)\}
\end{align} ∥ G ( s ) ∥ ∞ = ω sup σ { G ( jω )} ただし、
σ { G ( j ω ) } \sigma\{\bm{G}(j\omega)\} σ { G ( jω )} は
G ( j ω ) \bm{G}(j\omega) G ( jω ) の最大特異値を表し、
G ( j ω ) \bm{G}(j\omega) G ( jω ) の随伴行列を
G ∗ ( j ω ) \bm{G}^{\ast}(j\omega) G ∗ ( jω ) として与えられる以下の行列
A \bm{A} A の最大固有値の平方根となる。
A = G ( j ω ) G ∗ ( j ω ) \begin{align}
\bm{A} = \bm{G}(j\omega)\bm{G}^{\ast}(j\omega)
\end{align} A = G ( jω ) G ∗ ( jω ) システムがプラント変動に対して安定性と性能を保持するとき、ロバスト性能を有するという。安定性と性能を決定するパラメータは感度関数と相補感度関数となり、両方を独立に最適化することはできない。そのため、周波数帯域による感度・相補感度関数の割当てを行う必要がある。
指令値追従特性について、高周波数領域では入力飽和や位相遅れの影響から性能劣化を避けられないが、低周波数領域では性能を確保する必要がある。つまり、感度関数
S \bm{S} S は低周波数領域で
0 \bm{0} 0 近傍の値、高周波数領域で
I \bm{I} I 近傍の値を取ることが望ましい。一方の安定性について、モデル誤差は高周波数領域において発生しやすいため、相補感度関数
T \bm{T} T は高周波数領域で
0 \bm{0} 0 近傍の値、低周波数領域で
I \bm{I} I 近傍の値を取ることが望ましい。これを定式化するために重み関数
W S , W T \bm{W}_{\bm{S}}, \bm{W}_{\bm{T}} W S , W T を導入し、ロバストな制御系の条件を次のように記述する。
∥ S W S ∥ ∞ < 1 , ∥ T W T ∥ ∞ < 1 \begin{align}
\| \bm{S}\bm{W}_{\bm{S}} \|_{\infty} \lt 1,\ \| \bm{T}\bm{W}_{\bm{T}} \|_{\infty} \lt 1
\end{align} ∥ S W S ∥ ∞ < 1 , ∥ T W T ∥ ∞ < 1 この問題を個別に考えることは煩雑であるため、次のように定式化する。
∥ [ S W S T W T ] ∥ ∞ < 1 \begin{align}
\left \| \begin{bmatrix} \bm{S}\bm{W}_{\bm{S}} \\ \bm{T}\bm{W}_{\bm{T}} \end{bmatrix} \right \|_{\infty} \lt 1
\end{align} [ S W S T W T ] ∞ < 1 この問題は混合感度問題と呼ばれる。
H ∞ H_{\infty} H ∞ ノルムを
1 1 1 以下とする制御器が見つかればシステムはロバストな系となり、さらに小さい
H ∞ H_{\infty} H ∞ ノルムを与える制御器は安定度の高い制御系を構築する。