制御器設計によって実現可能な制御性能は、制御対象の物理的特性や駆動系およびセンサ系を含む制御対象の入出力機構に強く依存する。これは制御系が参照入力を生成してから応答を観測するまでの間に、駆動系の遅れ、制御対象の入出力遅れ、センサ系の観測遅れや雑音除去による推定遅れ等の遅れ要素が存在するためである。これらの遅れ要素に起因する制御性能の劣化は補償器設計のみで解決することが難しく、ソフトウェア・ハードウェアの統合的な設計によって性能向上を図る必要がある。

以下の制御器とプラント、およびその駆動系と観測系を含むシステムについて考える。ただし、$P, C, F$ はプラント、制御器、雑音除去フィルタ、$G_{\rm drv}, G_{\rm sen}$ は駆動系および観測系の伝達特性を表し、$r, u, y, d, v, w$ は指令値、入力、応答、外乱、駆動雑音および観測雑音を表す。このシステムに含まれる全ての要素は安定であるとし、一巡伝達関数は不安定極を持たないものとする。また、添字 $\ \hat{}\$ は推定値を表すものとする。

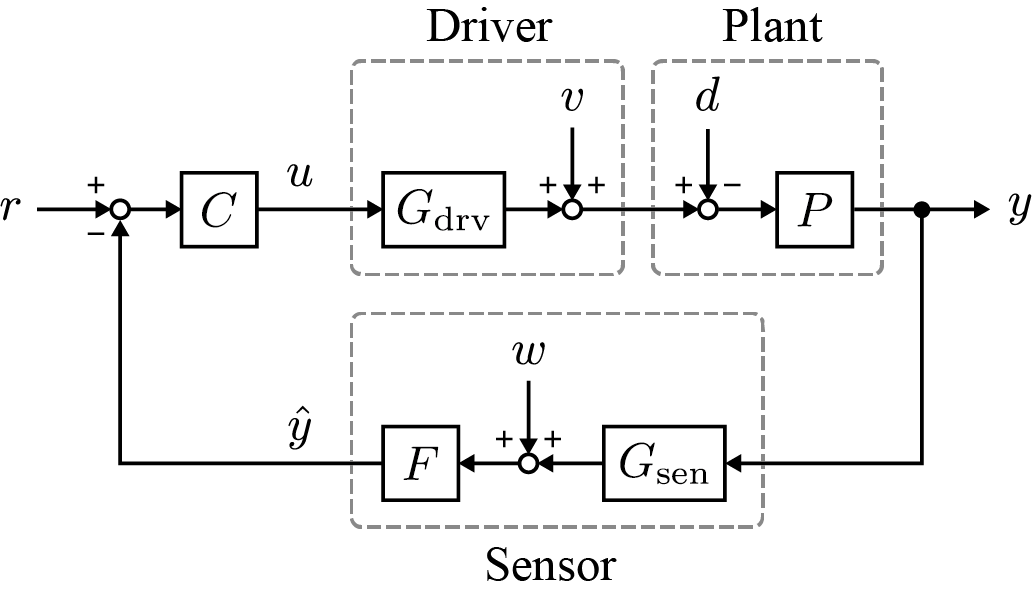
制御器から見たシステムの入出力特性はプラント本来の特性のみではなく、駆動系と観測系を含むものとなる。この入出力特性を $P_{\rm c}$ として次のように定義する。

このとき、一巡伝達関数 $L$ は次のように表される。

制御目標は広周波数帯域において応答を指令値に一致させることであり、指令値追従特性と外乱抑圧特性を向上するためにループゲインを高く設定する必要がある。しかしながら、ループゲインは一巡伝達関数内の位相遅れと重畳する雑音によって制限される。一巡伝達経路に存在する位相遅れは位相クロスオーバ周波数を低下させるため、ゲイン余裕を確保することが困難となる。位相遅れはプラントの伝達遅れ、駆動系のエネルギ生成遅れ、観測系の雑音除去フィルタによる遅れなど様々な要因で発生し、実設計においては制御器から見た一巡伝達関数 $P_{\rm c}$ を考慮しなければならない。また、応答に表れる雑音の影響はループゲインに依存し、ループゲインを高く設定した場合に応答の精度が劣化する可能性がある。雑音の影響は雑音除去フィルタによって低減することが可能であるが、除去フィルタによる位相遅れにより安定余裕度が減少するため、ループゲインの制限を取り除くことは困難となる。本稿では位相条件に起因する性能劣化と位相条件の緩和方法について紹介する。

動的システムの入出力は必ず位相遅れを伴い、システムの規模が大きくなるにつれて一巡経路における位相遅れが増加する。制御系を構築する場合にはシステムの状態に作用する駆動系、および状態を取得する観測系を設置する必要があり、一巡伝達特性はプラント本来の伝達特性にこれらの伝達特性を追加したものとなる。結果として、プラントの伝達特性のみを考慮して設計された制御系が不安定化する、もしくは性能が劣化する等の問題が発生する。

以下に示すPI制御器を有する速度制御系について考える。ただし、$J_{\rm m}, \omega_{\rm n}$ は慣性および閉ループ系の目標固有角周波数を表し、添字 $_{\rm n}\$ はモデル値を示すものとする。このシステムは駆動系に遅れ時間 $t_{\rm d}$ の伝達遅れが存在するものとし、状態の観測には遅れがないものとする。

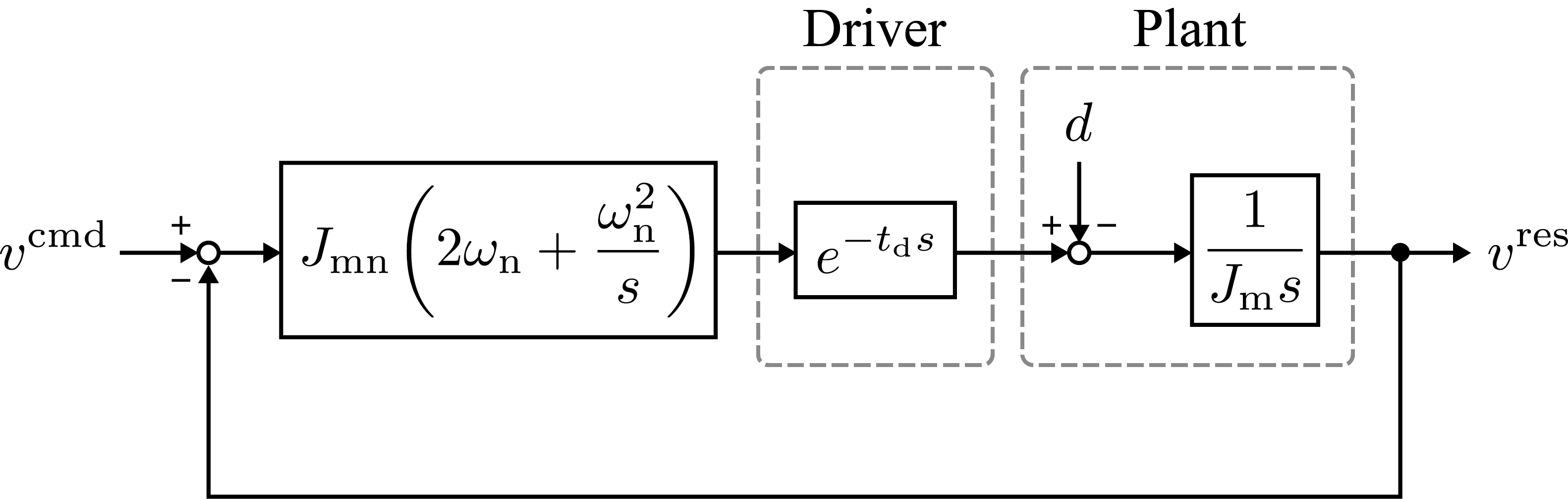
簡単のためモデル誤差が存在しない系を想定し、$J_{\rm m}=J_{\rm mn}$ として扱う。ここで、このフィードバック制御系の閉ループ伝達関数は以下のようになる。

遅れ時間が十分に小さく、固有角周波数 $\omega_{\rm n}$ を含む広い周波数帯域において時間遅れ要素による位相遅れが十分に小さい場合に、このシステムは減衰率 $1$、固有角周波数 $\omega_{\rm n}$ の二次遅れ特性を示す。しかしながら、時間遅れ要素による位相遅れ量が低周波数帯域で無視できない場合には安定余裕度の劣化が表れる。制御器が目標固有角周波数 $120.0\ {\rm rad/s}$を持ち、駆動系が $0.0, 1.5, 3.0, 4.5\ {\rm ms}$ の遅れ時間を有する場合に、ステップ応答およびステップ外乱応答は次のようになる。

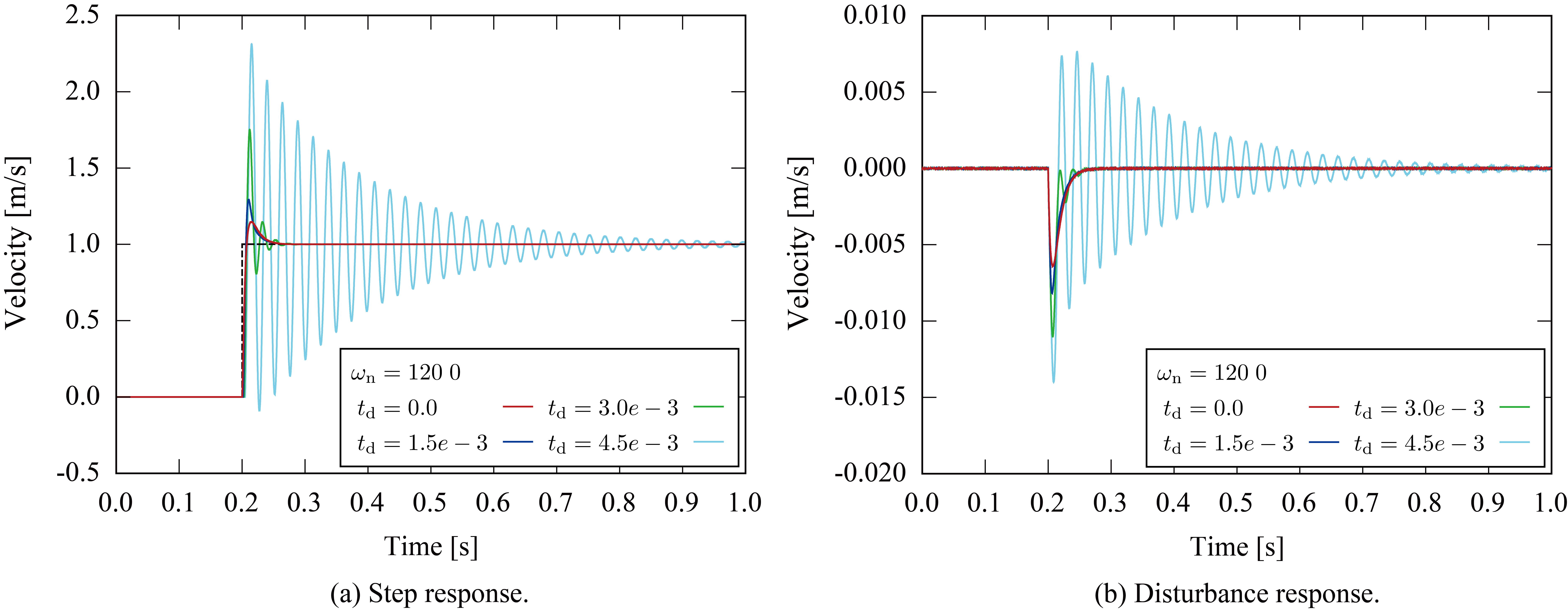
所望の減衰率を $1$ と設定しているが、時間遅れが存在する場合には応答が振動的になることが確認できる。これらの応答について、応答速度の変化は微小であり、減衰率のみ減少しているため、フィードバック系の極が複素右半平面側に向かって移動していると考えられる。ここで、一巡伝達関数のボード線図とナイキスト線図は以下のようになり、時間遅れ量の増加に伴い安定余裕度の減少が確認できる。

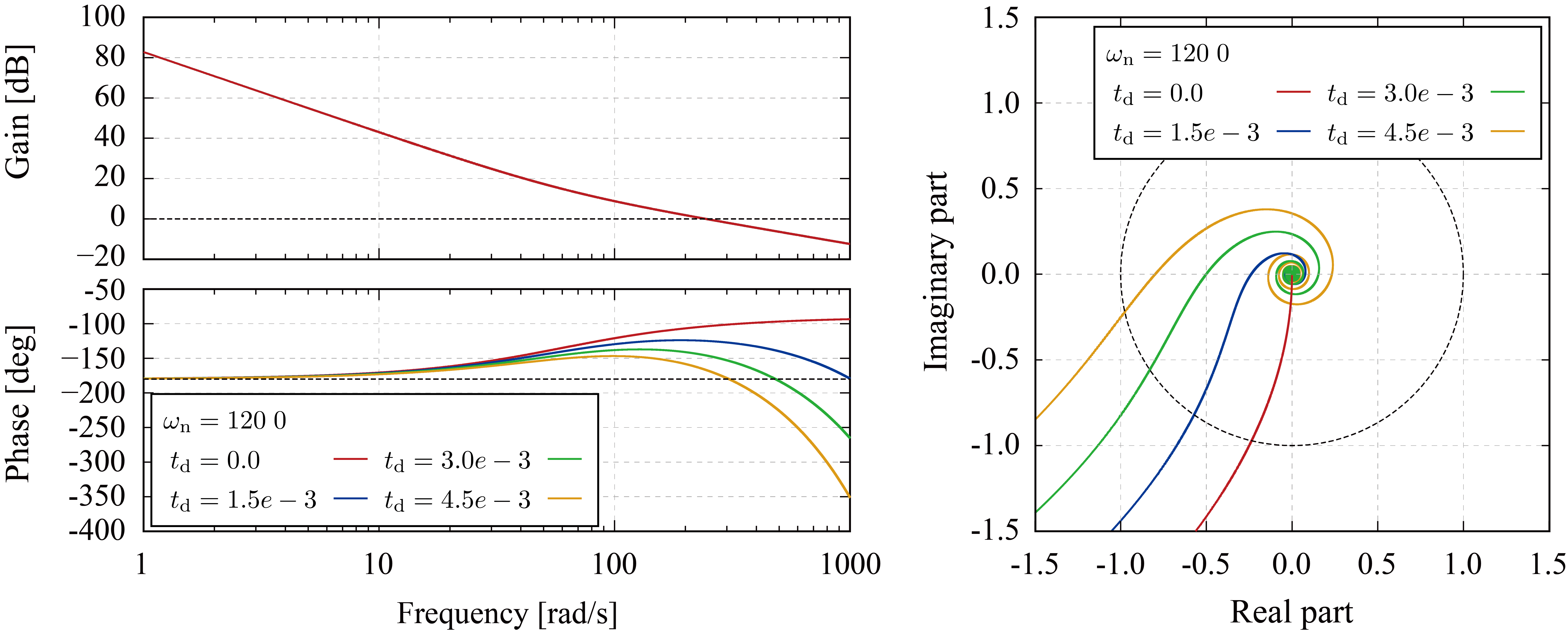
続いて、駆動系が遅れ時間 $4.5\ {\rm ms}$ を持つものとして、ループゲインを減少させることで安定余裕度を確保することを考える。以下に目標固有角周波数を $60.0, 80.0, 100.0, 120.0\ {\rm rad/s}$ と設定した場合のステップ応答およびステップ外乱応答を示す。

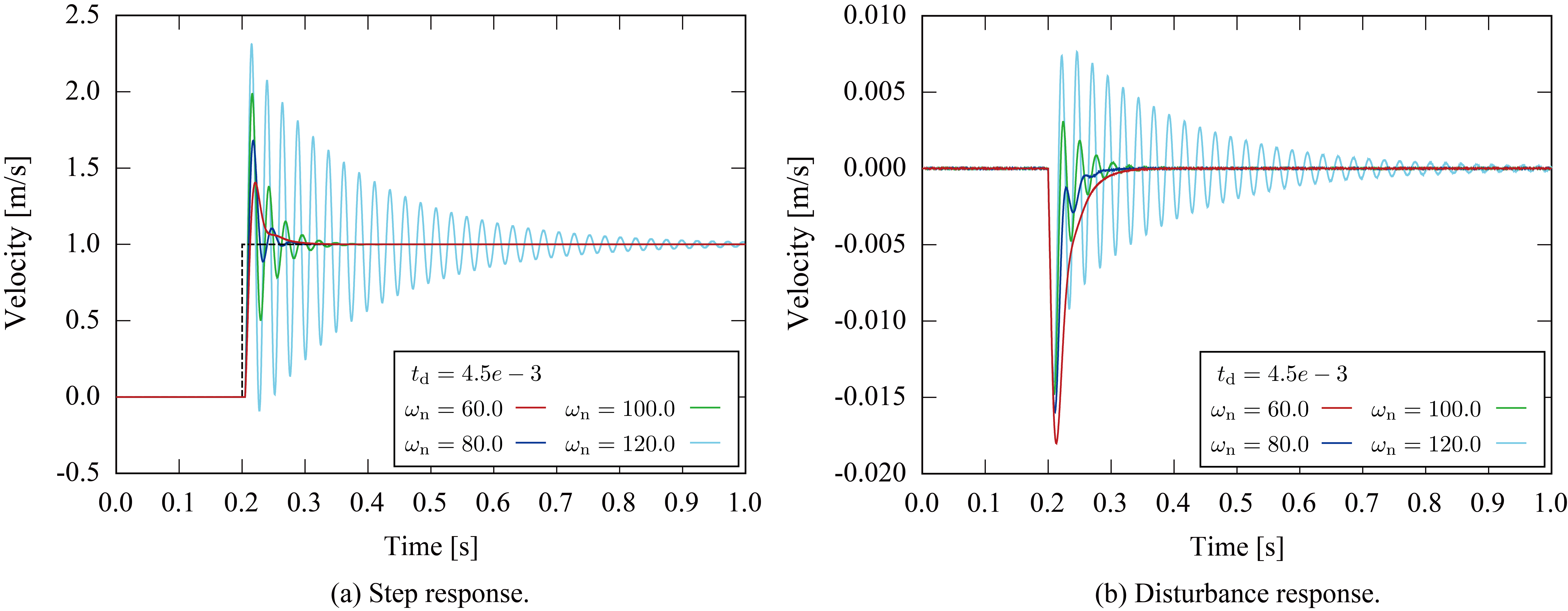
目標固有角周波数が減少するにつれて応答速度は減少するが、振動の収束時間が短縮することが確認できる。ここで、振動が十分に抑制された応答を得るためには、目標固有角周波数が強く制限される。これらのシステムの一巡伝達関数のボード線図とナイキスト線図は以下のようになる。

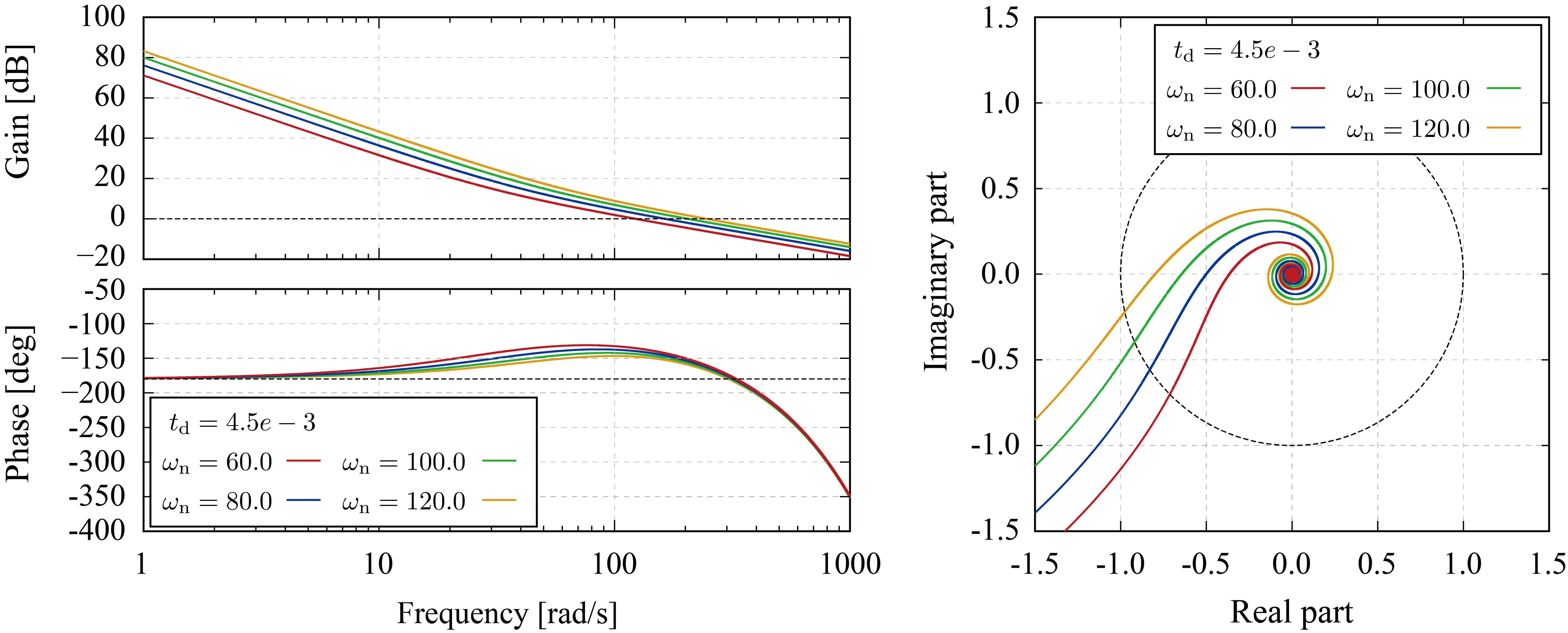
時間遅れ要素によって位相クロスオーバ周波数が低い値となり、今回設定した目標固有角周波数の範囲ではゲイン余裕が十分に確保できていないことが確認できる。このように位相遅れ要素はループゲインを制限するものとなり、フィードバック系の制御性能を制限する。

システムの物理特性に起因する伝達遅れは、制御器設計で補償することは難しく、そのシステムを改善することで対処することが望ましい。ここでは機械系の改善例として、共振現象を示す二慣性系を対称に入出力位相遅れの低減方法を検討する。対称とする二慣性系のブロック線図は以下のように表されるものとする。ただし、$f, x_1, x_2$ は作用力、作用点位置および終端位置を示し、$m, d, k$ はそれぞれ質量、粘性および剛性を表すものとする。

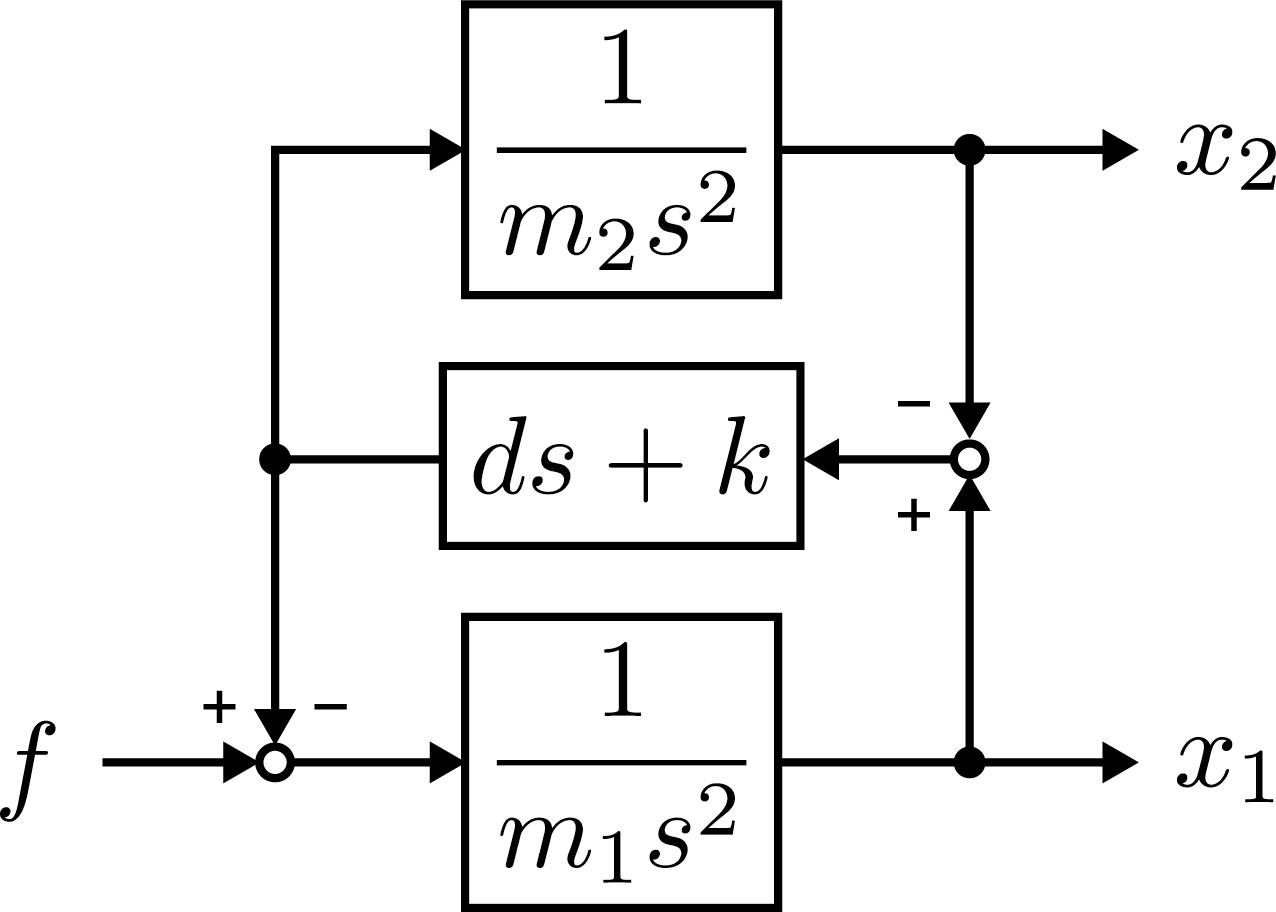
このシステムの $f$ から $x_2$ までの伝達関数 $G_{\rm p}$ は次のように表される。

ここで、$M$ は剛体系としての質量を表す。この系は低周波数帯域では質量 $M$ の剛体として振るまい、高周波数帯域では二慣性系の性質を示す。共振周波数 $\omega_{\rm r}$ は質量および剛性に依存し、この周波数によって剛体モードの周波数帯域が決定する。

これを確認するために、質量 $m_1 = m_2 = 0.5$、粘性 $d=2.0$ と設定し、剛性 $k=10000.0\sim 40000.0$ と変化させた場合のボード線図を以下に示す。

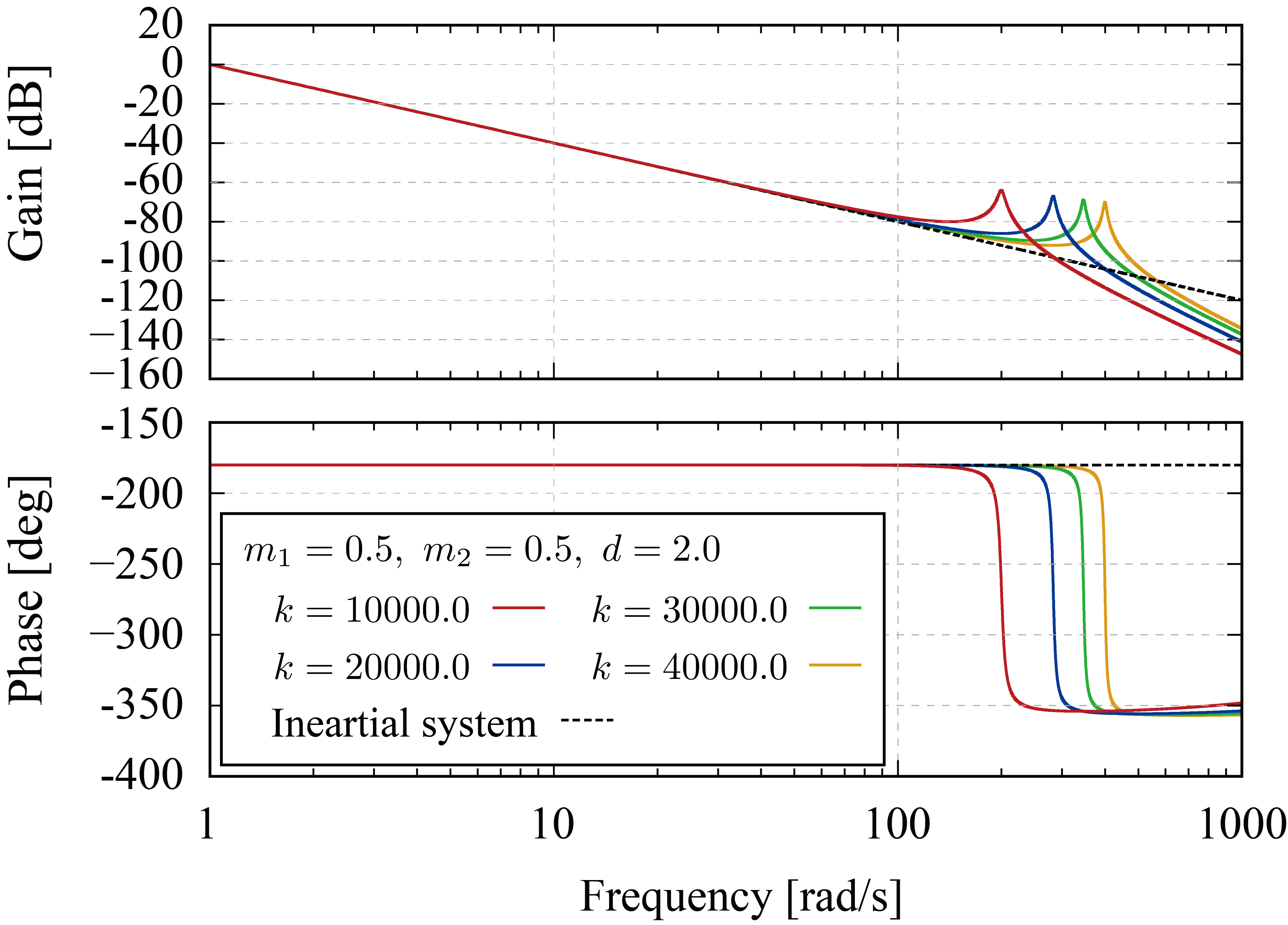
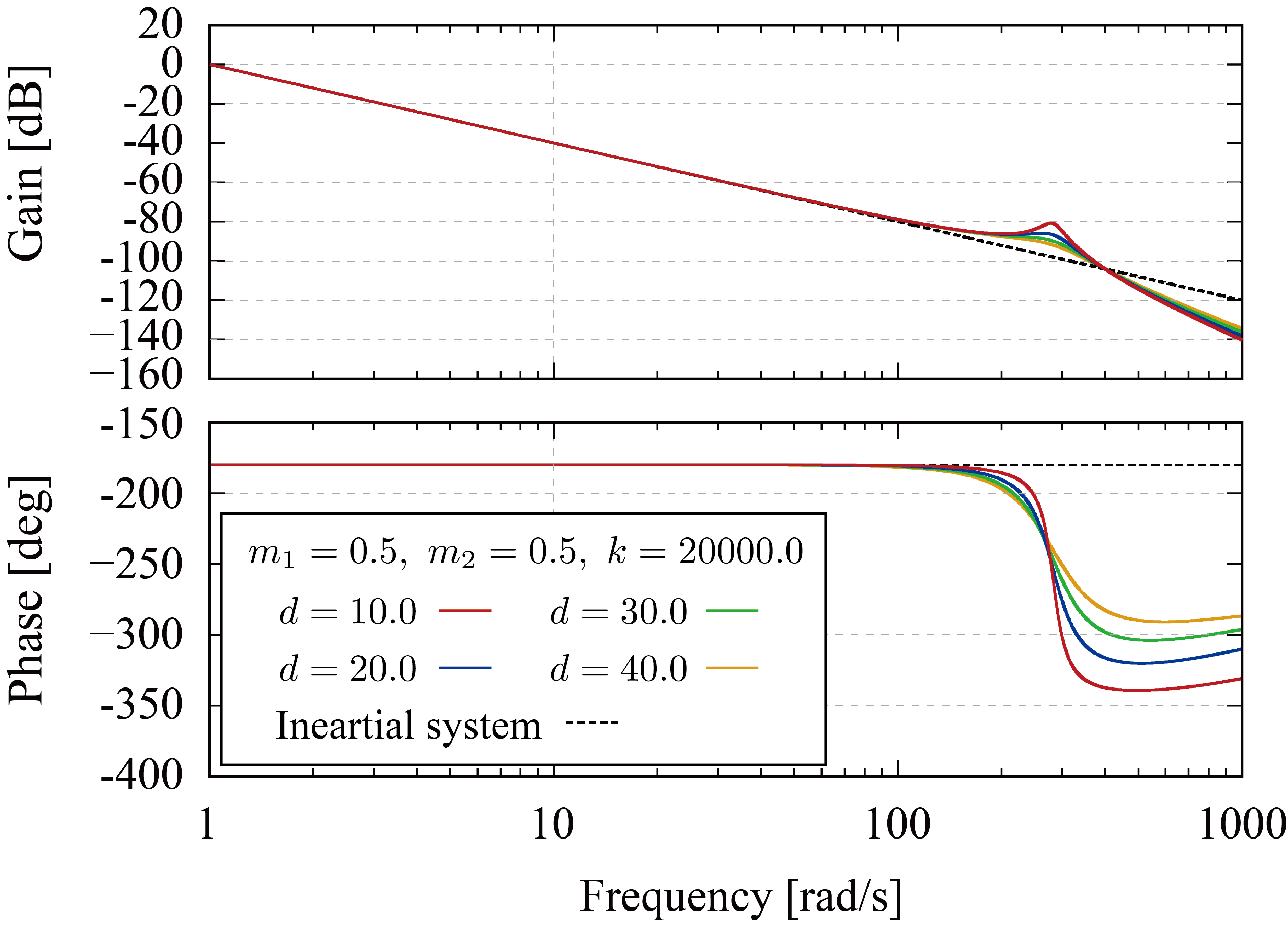
理想的な単慣性系による位相遅れ量 $-\pi$ に対して、共振系は共振周波数以降の周波数帯域において位相遅れを伴う。一方で、系は共振周波数以下の周波数帯域で剛体として振るまうことが確認できる。したがって、系の高剛性化および軽量化によって剛体モードの周波数帯域が広がり、位相変動の影響を低減することができる。また、粘性を付加することで系の減衰率を増加し、振動ピークを抑えることで系の特性を剛体系に近づけることができる。以下に質量 $m_1 = m_2 = 0.5$、剛性 $k=20000.0$ と設定し、粘性 $d=10.0\sim 40.0$ と変化させた場合のボード線図を示す。この結果は粘性の増加に伴って振幅ピークと位相遅れが低減することを表しており、防振材の設置が位相特性の改善に有効であることを示している。

無人航空機 (Unmanned Aerial Vehicle: UAV) は姿勢の安定性や外乱に対するロバスト性など高い制御性能が要求されるアプリケーションである。本稿ではクアッドロータ型UAVの姿勢制御系の設計例を紹介する。

クアッドロータ型UAVは、4つのアーム先端に設置されたモータとプロペラによって発生する推力を使用して姿勢の安定化および移動を行う。姿勢の推定は慣性計測装置 (Inertial Measurement Unit: IMU) および地磁気センサを使用して行われ、これらのセンサは機体中央部に設置される。この動作はブロック線図を用いて次のように表現される。

ここで、$\Phi, T$ は姿勢角およびプロペラによる推力を表し、添字 $_{\rm ref},\ _{\rm sen}$ は参照値および観測値を示すものとする。推力制御系はモータの回転速度制御系と回転数-発生推力のマップを持ち、推力参照値に対してモータ回転数を調整する役割を持つ。この系に対して姿勢制御系を構築するとき、制御系のブロック線図は次のように表される。

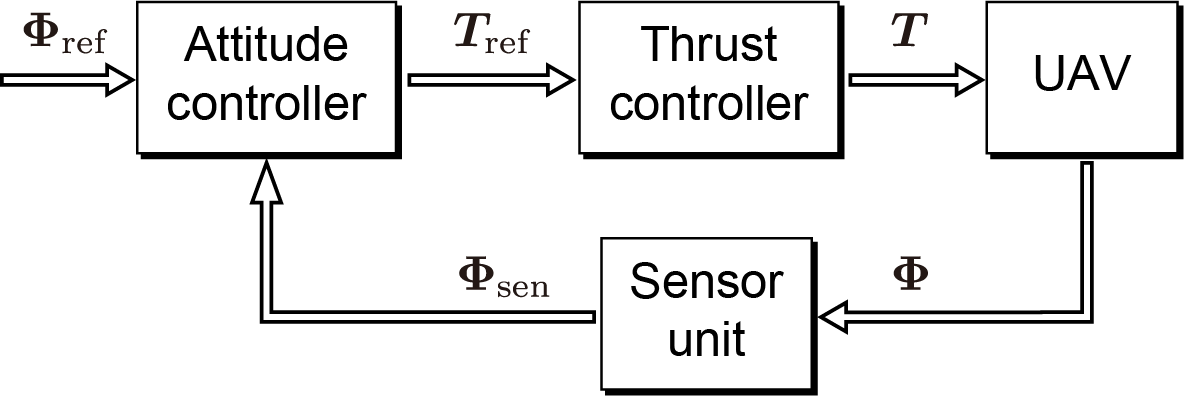
姿勢制御系の構築について、実現可能な安定化制御器は推力参照値から姿勢角観測値までの開ループ伝達関数によって決定される。高い姿勢安定性と外乱抑圧性能を確立するためには、機体が広い周波数帯域で剛体系として動作し、推力発生と姿勢角測定の遅れが小さいことが望ましい。

UAVのアームは片持ち梁となるため振動が発生しやすく、高剛性化や防振材の設置が必要となる。前述の写真の機体では機体中心部とアームの接続部に防振材が挿入されており、機械振動が低減されている。

推力制御系の応答性はモータの回転速度制御系の性能に依存する。この回転速度制御系を搭載したシステムはElectric Speed Controller (ESC) と呼ばれる。UAV用途のESCでは120度通電によるモータ駆動方式が採用されているが、回転速度制御系の応答性の向上が難しく、推力発生に遅れが発生する。これに対して、ベクトル制御によるモータ駆動方式では回転制御系の応答の高速化が可能であり、推力発生の遅れを低減することができる。UAVに搭載されているモータに対して2つの駆動方式でモータ回転数を制御し、$4000\ {\rm rpm}\rightarrow 5000\ {\rm rpm}$ と変化させた場合の推力応答を以下に示す。

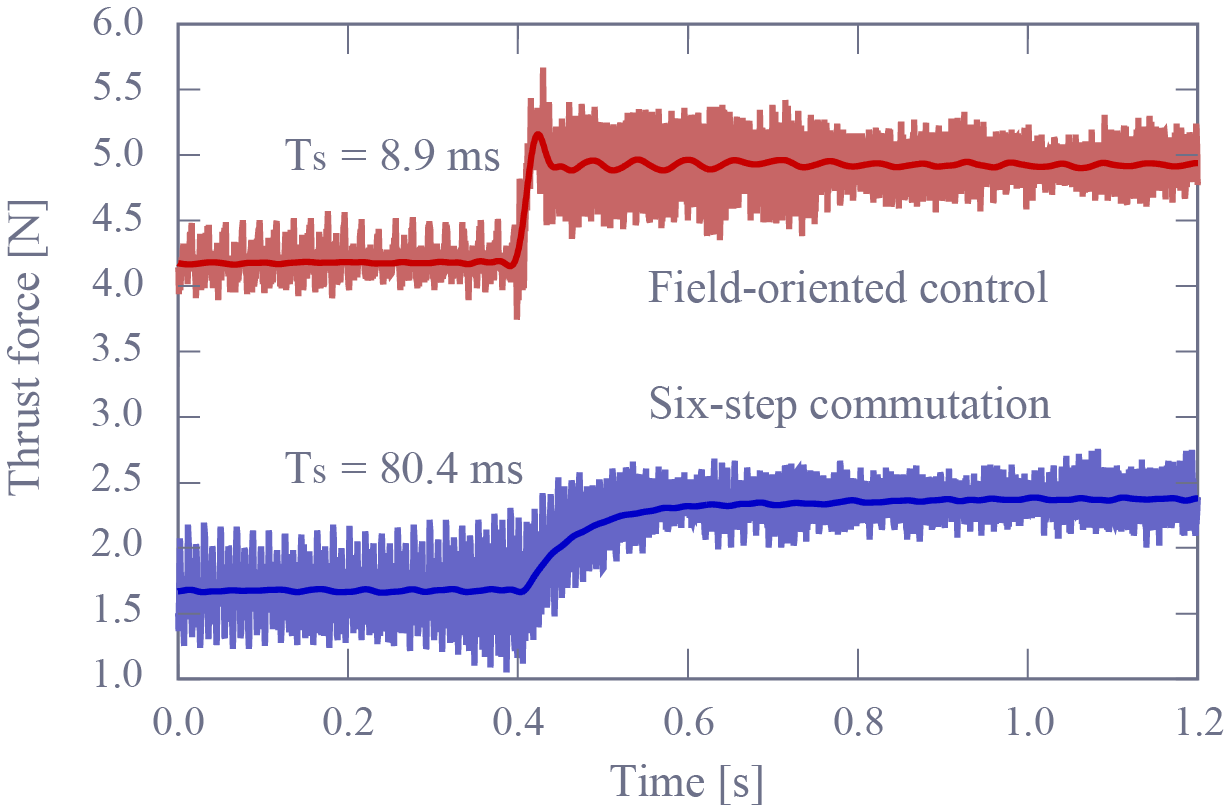
それぞれの駆動方式によって得られた推力応答の時定数は $8.9\ {\rm ms}$ および $80.4\ {\rm ms}$ となり、ベクトル制御方式の採用により時定数が $89.0\ \%$ 低減することが確認された。

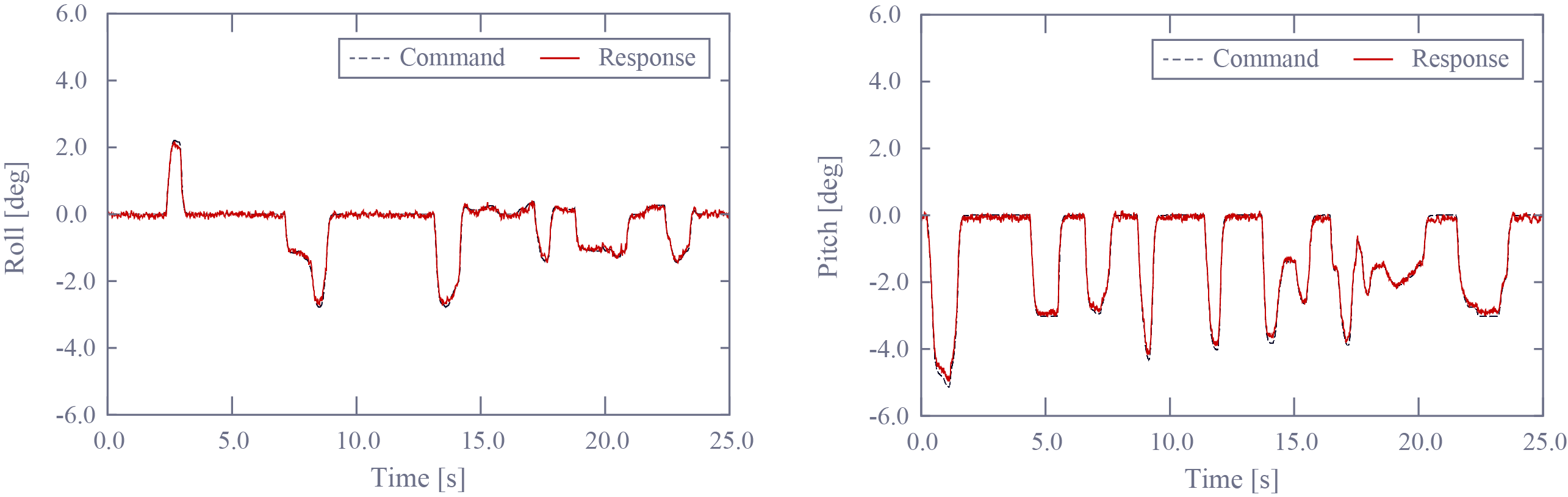
推力参照値から姿勢角までの開ループ伝達特性を改善することにより姿勢制御器の設定可能なゲインの上限値が増加し、制御系の周波数特性が向上する。UAVに対して二自由度制御器を導入し、姿勢角参照値を与えた際の応答を以下に示す。急峻な指令値変化に応答が追従し、一定指令値に対して追従誤差が抑圧されているため、制御周波数帯域の広帯域化が確認できる。