極と零点 | DigitalServo

極と零点

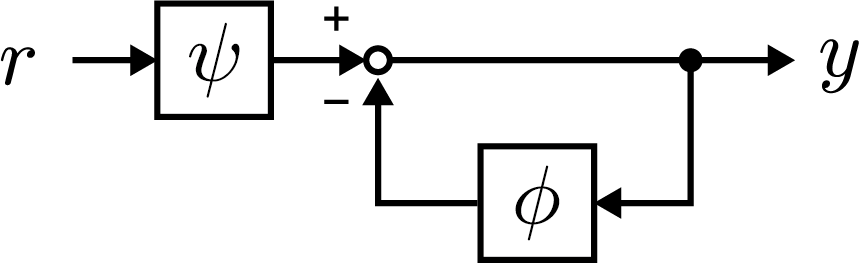
有理関数形式で表現される伝達関数について、分母多項式の根を極、分子多項式の根を零点と呼ぶ。極と零点はシステムの周波数特性の特徴量であり、システムの特性を推測するために使用することができる。ここでは極と零点がシステムの応答にどのような影響を与えるかについて述べる。

極と零点の役割

伝達関数

G

が多項式

\psi, \phi

を用いて次の形式で表現される場合について考える。

\begin{align} G(s) = \frac{\psi(s)}{1 + \phi(s)} \end{align}

この伝達関数を実現する以下の代数方程式とブロック線図について確認すると、分子多項式は入力伝達特性に作用しており、分母多項式はシステムのダイナミクスを表現していることがわかる。ここで、

r, y

はそれぞれ入力および出力であり、

u

は媒介変数とする。

\begin{align} u &\equiv \psi r \\ y &= \frac{1}{1 + \phi} u \end{align}

したがって、極および零点から入出力伝達特性を推測することができる。

極による動特性の確認

代数学の基本定理より一変数を持つ実数係数多項式は一次および二次の実因子に分解可能であることが示されており、任意の有理関数は分母多項式の各因子を分母とする分数の総和として表現することができた。簡単のため、重複しない実数

a_i\ (i=1,...,n)

と複素共役対

b_i, \bar{b}_{i}\ (i=1,...,m)

を極に持つ伝達関数

G(s)

について考えると、この伝達関数は適当な複素係数多項式

c_{i}(s), d_{i}(s)

を用いて次のように表現することができる。

\begin{align} G(s) &= \sum^{n}_{i=1} \frac{c_{i}}{s + a_{i}} + \sum^{m}_{i=1} \frac{d_{i}}{(s + b_{i})(s + \bar{b}_{i})} \\ &= \sum^{n}_{i=1} \frac{c_{i}}{s + a_{i}} + \sum^{m}_{i=1} \frac{d_{i}}{s^2 + 2\zeta_{i}\omega_{\rm i}s + \omega_{\rm i}^2}, \\ \zeta_{i} &= \frac{b_{1} + \bar{b}_{i}}{2|b_{i}|}\\ \omega_{i} &= |b_{i}| \end{align}

入力を

x

、出力を

y

とすると、出力は以下のようになる。

\begin{align} y(t) &= \sum^{n}_{i=1} \frac{c_{i}}{s + a_{i}}x(s) + \sum^{m}_{i=1} \frac{d_{i}}{s^2 + 2\zeta_{i}\omega_{\rm i}s + \omega_{\rm i}^2} x(s) \\ \rightarrow y(t) &= \sum^{n}_{i=1} \mathcal{L}^{-1}\left[ \frac{c_{i}}{s + a_{i}}x(s)\right] + \sum^{m}_{i=1} \mathcal{L}^{-1}\left[ \frac{d_{i}}{s^2 + 2\zeta_{i}\omega_{\rm i}s + \omega_{\rm i}^2} x(s)\right] \end{align}

したがって、出力応答は分解された一次遅れ系および二次遅れ系に入力を行った際の出力の総和となり、一次遅れ系と二次遅れ系の特性のみから高次システムの動作が推測可能であることを示している。遅れ系の特性として、実数極を持つ一次遅れ系は極の位置から応答の減衰速度を、複素共役対の極を持つ二次遅れ系は固有角周波数と減衰率から応答の振動周波数と振動持続性を確認することができる。システムの動特性が極に依存することから、伝達関数の分母多項式は特性多項式と呼ばれる。

支配極の影響

正の実数

a, b

に対して

-a, -b

を極に持つ以下の二次遅れ系

G(s)

について考える。

\begin{align} G(s) &= \frac{ab}{(s+a)(s+b)} \end{align}

このシステムのインパルス応答

y(t)

は、ヘヴィサイドの展開定理より次のように記述される。

\begin{align} y(t) &= \frac{ab}{-a+b}e^{-at} + \frac{ab}{-b+a}e^{-bt} \\ &= \frac{ab}{b - a} \left( e^{-at} - e^{-bt} \right) \\ &= \frac{ab}{b - a} e^{-at} \left( 1 - e^{-(b - a)t} \right) \\ \end{align}

ここで、

b

が

a

に対して十分に大きい場合に、インパルス応答を次のように近似することができる。

\begin{align} y(t) &= \frac{a}{1 - \frac{a}{b}} e^{-at} \left( 1 - e^{-(b - a)t} \right) \approx ae^{-at}\\ \end{align}

これは次の伝達関数

G_{r}(s)

のインパルス応答を表す。

\begin{align} G_{r}(s) &= \mathcal{L}\left[ae^{-at}\right] = \frac{a}{s+a} \end{align}

システムの本来の伝達関数

G(s)

について確認すると、低周波数帯域では近似的に上記の伝達特性を示すことが確認できる。

\begin{align} G(s) &= \frac{a}{(s+a)(\frac{1}{b}s+1)} = \frac{1}{\frac{1}{b}s+1}G_{r}(s) \\ &\approx G_{r}(s) \end{align}

この結果から、大域的な応答速度は原点から近い極に支配されることがわかる。このような極を支配極と呼ぶ。したがって、システムの応答性を向上するためには原点から最も近い距離にある極について対処する必要がある。

零点による入力伝達特性の変化

n

個の零点を持つ伝達関数は

n

次の分子多項式を持つ。実数係数

a_i\ (i= 0, ..., n)

を持つ分子多項式と特性多項式

\phi(s)

から構成される次の伝達関数を考える。

\begin{align} G(s) &\equiv \frac{\sum^{n}_{i=0} a_{i}s^{i} }{\phi (s)} \end{align}

ここで、以下の初期条件を満たす入力を

x

、出力を

y

としてシステムの入出力特性を確認する。

\begin{align} \frac{d^k}{dt^k}x(0) &= 0\ (k=0,...,n-1) \\ \rightarrow s^k x(s) &= \mathcal{L}\left[ \frac{d^k}{dt^k}x(t) \right] \end{align}

ここで、出力

y

のラプラス変換は次のように記述される。

\begin{align} y(s) &= \frac{1}{\phi (s)} \sum^{n}_{i=0} a_{i}s^{i}x(s) \\ &= \frac{1}{\phi (s)} \sum^{n}_{i=0} \mathcal{L}\left[ \frac{d^i}{dt^i} a_{i}x(t) \right] \end{align}

この表現から、伝達関数に零点が存在する場合には入力の高次導関数が出力に影響することが確認できる。そのため、急峻な入力に対して出力のオーバーシュート、アンダーシュートといった問題が発生する。

不安定零点による非最小位相特性

安定零点

p_i\ (i= 1, ..., n_1)

、不安定零点

q_j\ (j= 1, ..., n_2)

、および安定極

r_k\ (k= 1, ..., n_3)

を有する以下のシステムについて考える。

\begin{align} G(s) &\equiv \frac{\prod^{n_1}_{i=1}(s + p_{i}) \prod^{n_2}_{i=1}(-s + q_{i}) }{\prod^{n_3}_{i=1}(s + r_{i})} \\ \end{align}

この有理関数は次のように展開することができる。

\begin{align} G(s) &= (-1)^{n_{2}} \left( \prod^{n_2}_{i=1}\frac{s + q_{i}}{s + q_{i}} \right) \frac{\prod^{n_1}_{i=1}(s + p_{i}) \prod^{n_2}_{i=1}(s - q_{i}) }{\prod^{n_3}_{i=1}(s + r_{i})}\\ &= (-1)^{n_{2}} \left( \prod^{n_2}_{i=1}\frac{s - q_{i}}{s + q_{i}} \right) \frac{\prod^{n_1}_{i=1}(s + p_{i}) \prod^{n_2}_{i=1}(s + q_{i}) }{\prod^{n_3}_{i=1}(s + r_{i})}\\ \end{align}

ここで伝達関数

G(s)

を有理関数

A(s)

と安定零点のみを持つ伝達関数

G_{\rm o}(s)

の積として表現する。

\begin{align} G(s) &= A(s) G_{\rm o}(s) \\ A(s) &\equiv \prod^{n_2}_{i=1}\frac{-s + q_{i}}{s + q_{i}}\\ G_{\rm o}(s) &\equiv \frac{\prod^{n_1}_{i=1}(s + p_{i}) \prod^{n_2}_{i=1}(s + q_{i}) }{\prod^{n_3}_{i=1}(s + r_{i})} \end{align}

このとき、有理関数

A(s)

は一定の増幅率を持ち位相のみを変化させる全域通過フィルタとなる。

\begin{align} A(j\omega) &\equiv \prod^{n_2}_{i=1}\frac{-j\omega + q_{i}}{j\omega + q_{i}}\\ &= \prod^{n_2}_{i=1} \frac{\sqrt{\omega^2 + q_{i}^2}e^{-j\tan^{-1}(\omega / q_{i})}}{\sqrt{\omega^2 + q_{i}^2}e^{j\tan^{-1}(\omega / q_{i})}}\\ &= \prod^{n_2}_{i=1} e^{-j2\tan^{-1}(\omega / q_{i})}\\ |A(\omega)| &= 1\\ \angle A(\omega) &= - 2\sum^{n_{2}}_{i=1} \tan^{-1}\left(\frac{\omega}{q_{i}}\right) \end{align}

したがって、伝達関数

G(s)

の振幅・位相特性は次のように表される。

\begin{align} |G(\omega)| &= |A(\omega)G_{\rm o}(\omega)| = |G_{\rm o}(\omega)|\\ \angle G(\omega) &= \angle G_{\rm o}(\omega) + \angle A(\omega) = \angle G_{\rm o}(s) - 2\sum^{n_{2}}_{i=1} \tan^{-1}\left(\frac{\omega}{q_{i}}\right) \end{align}

この結果から、同一の振幅特性を有する伝達関数のうち、安定零点のみを持つシステムが最小の位相遅れ特性を示すことが確認できる。そのため、安定零点のみを持つシステムは最小位相系と呼ばれ、

G_{\rm o}(s)

はアウター関数と呼ばれる。一方で不安定零点は入出力の位相遅れの原因となり、不安定零点を持つシステムは非最小位相系と呼ばれる。伝達関数を全域通過フィルタとアウター関数の積として表現することをインナー・アウター展開と呼ぶ。非最小位相系に対してフィードバック制御系を構築する場合、一巡伝達関数に位相遅れが含まれるため安定性の確保や制御帯域の広域化が困難となる。

CONTENTS