DigitalServo

Blog

About

Library

    線形制御系設計

    線形システムの表現
    線形システムの特性解析
    制御器設計
    観測器設計

    モーションコントロール

    加速度制御
    剛体の姿勢制御

    モータドライブ

    駆動制御法
    磁極位置推定法

    システム同定

    ホワイトボックスモデル

ナイキスト線図を用いた安定性解析

ナイキスト線図はフィードバック制御系の安定性を視覚的に確認するために使用される。システムの安定性は、特性方程式の全ての根が複素左半平面に存在することであり、この条件は一巡伝達関数の振幅・位相特性から判定することが可能であることが証明されている。ナイキスト線図は一巡伝達関数を複素平面に図示したものとなり、視覚的に安定性とその安定余裕度を与える。ここではナイキストの安定判別法の原理と使用方法について述べる。

問題定義

一巡伝達関数が不安定な極零相殺を含まず、以下の有理関数形式で表現される場合について考える。
L=NL(s)DL(s) \begin{align} L = \frac{N_{\rm L}(s)}{D_{\rm L}(s)} \end{align}
ここで、LL は一巡伝達関数を表し、NL,DLN_{\rm L}, D_{\rm L} は共通因子を持たない実係数多項式とする。この一巡伝達特性を持つ経路で負帰還フィードバックを構成した場合、特性多項式 ϕ\phi は次のようになる。
ϕ(s)=1+L=NL+DLDL \begin{align} \phi (s) &= 1 + L = \frac{N_{\rm L} + D_{\rm L}}{D_{\rm L}} \end{align}
この特性多項式が不安定な零点を持たないことがシステムの安定条件となる。この特性多項式の分母多項式と分子多項式は次数の等しい実係数多項式となることに留意する。

コーシーの偏角の原理

偏角の原理は対数微分の周回積分によって有理型関数の零点と極の個数の差を与える。複素平面上の単純閉曲線 CC の囲む有界領域において、有理型関数 f(s)f(s) が重複するものも含めてそれぞれ p,qp, q 個の零点と極を持ち、 かつ経路 CC 上に極と零点を持たない場合に次の式が成立する。ただし、積分経路は CC を有界領域の内点から偏角が正の方向 (反時計周り) に進むものとする。
12πj∮Cf′(s)f(s)ds=p−q\begin{align} \frac{1}{2\pi j}\oint_{C} \frac{f'(s)}{f(s)}ds = p - q \end{align}

周回積分の解釈

複素多項式 f(s)f(s) の対数微分の周回積分は、f(s)f(s) の偏角の総変化量と捉えることができる。対数微分の周回積分は次のように変形することができる。
12πj∮Cf′(s)f(s)ds=12πj∮Cd(log⁡f(s))\begin{align} \frac{1}{2\pi j}\oint_{C} \frac{f'(s)}{f(s)}ds = \frac{1}{2\pi j}\oint_{C} d\left( \log f(s) \right) \end{align}
ここで、f(s)f(s) を以下のように極座標表示し、対数微分の周回積分を再び変換する。
f(s)≡r(s)ejθ(s)⇔log⁡f(s)=log⁡r(s)+log⁡ejθ(s)=log⁡r(s)+jθ(s)⇔d(log⁡f(s))=d(log⁡r(s))+jθ˙(s)dθ∴12πj∮Cd(log⁡f(s))=12πj(∮Cd(log⁡r(s))+∮Cjθ˙(s)dθ)\begin{align} f(s) & \equiv r(s)e^{j\theta(s)} \\ \Leftrightarrow \log f(s) &= \log r(s) + \log e^{j\theta(s)}\\ &=\log r(s) + j\theta(s) \\ \Leftrightarrow d\left( \log f(s) \right) &= d\left(\log r(s)\right) + j\dot{\theta}(s)d\theta \\ \therefore \frac{1}{2\pi j}\oint_{C} d\left( \log f(s) \right) &= \frac{1}{2\pi j} \left(\oint_{C} d\left(\log r(s)\right) + \oint_{C} j\dot{\theta}(s)d\theta \right) \end{align}
ここで、r,θr, \theta は複素多項式 ff のノルムと偏角を表現する複素多項式とする。周回積分の始点と終点は一致するためノルム rr は始点と終点で同値を持つ、すなわち積分区間におけるノルム rr の総変化は 00 となる。これはコーシーの積分定理の主張内容であり、閉曲線内の有界領域で関数が正則となる場合、その関数の周回積分の値は 00 となることが示されている。以上より、f(s)f(s) の対数微分の周回積分は次のように記述することができる。
12πj∮Cf′(s)f(s)ds=12π∮Cθ′(s)dθ\begin{align} \frac{1}{2\pi j}\oint_{C} \frac{f'(s)}{f(s)}ds &= \frac{1}{2\pi} \oint_{C} \theta'(s)d\theta \\ \end{align}

不安定極零点の個数判別

経路 CC が複素右半平面の全てを囲むとした場合に、不安定な零点と極の個数の差 kk は次のように計算される。
k=12πj∮Cf′(s)f(s)ds=12πj{lim⁡ω→∞∫jω−jωf′(jω)f(jω)dω+∫−π2π2lim⁡r→∞f′(rejθ)f(rejθ)dθ}=12πj{−lim⁡ω→∞∫−jωjωf′(jω)f(jω)dω+∫−π2π2d(lim⁡r→∞log⁡f(rejθ))}\begin{align} k &= \frac{1}{2\pi j}\oint_{C} \frac{f'(s)}{f(s)}ds \\ &= \frac{1}{2\pi j} \left\{ \lim_{\omega\rightarrow\infty}\int^{-j\omega}_{j\omega} \frac{f'(j\omega)}{f(j\omega)}d\omega + \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \lim_{r\rightarrow \infty} \frac{f'(re^{j\theta})}{f(re^{j\theta})}d\theta \right\} \\ &= \frac{1}{2\pi j} \left\{ -\lim_{\omega\rightarrow\infty}\int^{j\omega}_{-j\omega} \frac{f'(j\omega)}{f(j\omega)}d\omega + \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} d\left( \lim_{r\rightarrow \infty} \log f\left(re^{j\theta}\right) \right) \right\} \\ \end{align}
ここで、有理型関数 ff の分子多項式と分母多項式が共に nn 次の多項式であり、nn 個の極と零点を持つ場合について考える。極と零点をそれぞれ ai,zi(i=1,...n)a_{i}, z_{i} (i=1,...n) とし、ff を次のように記述する。
f(s)=K∏i=1n(s−zi)∏i=1n(s−ai)\begin{align} f(s) &= K\frac{\prod_{i=1}^{n} (s-z_{i})}{\prod_{i=1}^{n} (s-a_{i})} \end{align}
ただし、KK は定数とする。このとき、以下の式が成立することが確認できる。
∀θ∈R, lim⁡r→∞f(rejθ)=lim⁡r→∞K∏i=1n(rejθ−zi)∏i=1n(rejθ−ai)=lim⁡r→∞K∏i=1nrejθ∏i=1nrejθ=K\begin{align} \forall \theta \in \mathbb{R}, \ \lim_{r\rightarrow \infty} f\left(re^{j\theta}\right) &= \lim_{r\rightarrow \infty} K\frac{\prod_{i=1}^{n} (re^{j\theta}-z_{i})}{\prod_{i=1}^{n} (re^{j\theta}-a_{i})} \\ &= \lim_{r\rightarrow \infty} K\frac{\prod_{i=1}^{n} re^{j\theta}}{\prod_{i=1}^{n} re^{j\theta}} \\ &= K \end{align}
したがって、以下の式が成立する。
ddθ(lim⁡r→∞log⁡f(rejθ))=0\begin{align} \frac{d}{d\theta} \left( \lim_{r\rightarrow \infty} \log f \left(re^{j\theta}\right) \right) = 0 \end{align}
以上より、不安定な零点と極の個数の差 kk は次の広義積分によって計算される。
k=−12πjlim⁡ω→∞∫−jωjωf′(jω)f(jω)dω\begin{align} k &= -\frac{1}{2\pi j} \lim_{\omega\rightarrow\infty}\int^{j\omega}_{-j\omega} \frac{f'(j\omega)}{f(j\omega)}d\omega \end{align}

ナイキストの安定判別法

有理関数形式で表現される一巡伝達関数 ϕ\phi が重複するものも含めてそれぞれ pu,qup_{\rm u}, q_{\rm u} 個の不安定な零点と極を持つとき、以下の式が成立する。
−12πjlim⁡ω→∞∫−jωjωf′(jω)f(jω)dω=pu−qu\begin{align} -\frac{1}{2\pi j} \lim_{\omega\rightarrow\infty}\int^{j\omega}_{-j\omega} \frac{f'(j\omega)}{f(j\omega)}d\omega &= p_{\rm u} - q_{\rm u} \end{align}
システムが安定であるための条件は pu=0p_{\rm u}=0 であるため、安定条件は次のように記述される。
12πjlim⁡ω→∞∫−jωjωf′(jω)f(jω)dω=qu\begin{align} \frac{1}{2\pi j} \lim_{\omega\rightarrow\infty}\int^{j\omega}_{-j\omega} \frac{f'(j\omega)}{f(j\omega)}d\omega &= q_{\rm u} \end{align}
安定条件に含まれる広義積分を解析的な求解は一般に困難であるため、特性方程式を用いた図示による求解を行う。複素関数 ff の対数微分の周回積分は、ff の偏角 θ\theta の総変化量と見ることができた。そのため、以下の広義積分に関して次の変換が成立する。
12πjlim⁡ω→∞∫−jωjωf′(jω)f(jω)dω=12πlim⁡ω→∞∫−jωjωθ′(s)dθ\begin{align} \frac{1}{2\pi j} \lim_{\omega\rightarrow\infty}\int^{j\omega}_{-j\omega} \frac{f'(j\omega)}{f(j\omega)}d\omega &= \frac{1}{2\pi} \lim_{\omega\rightarrow\infty}\int^{j\omega}_{-j\omega} \theta'(s) d\theta \end{align}
右辺の広義積分は s=−j∞→+j∞s=-j\infty \rightarrow +j\infty とした際の特性多項式 ϕ(s)\phi(s) の偏角の総変化量であり、ϕ\phi を複素平面上に描き最終的な偏角を確認することで解を得ることができる。この軌跡はベクトル線図と呼ばれ、ベクトル線図が原点を反時計回りに 11 周することは偏角の総変化量が 2π2\pi となることを示し、 nn 周すると偏角の総変化量が 2nπ2n\pi となることを示す。ここで、線図が原点を反時計回りに nn 回転した場合の周回積分値は以下の値を取る。
12πlim⁡ω→∞∫−jωjωθ′(s)dθ=n\begin{align} \frac{1}{2\pi} \lim_{\omega\rightarrow\infty}\int^{j\omega}_{-j\omega} \theta'(s) d\theta = n \end{align}
したがって、特性多項式 ϕ\phi のベクトル線図が原点を反時計回りに回転する回数と一巡伝達関数の不安定零点の個数が一致することが、システムの安定条件となる。ここで、特性多項式 ϕ\phi と一巡伝達関数 LL が ϕ=1+L\phi = 1 + L の関係で結ばれることから、一巡伝達関数の線図から同様の安定判別を行うことができる。その場合、線図が複素平面上の点 (−1,j0)(-1, j0) を反時計回りに回転した回数を数える。この LL のベクトル線図をナイキスト線図と呼ぶ。

簡易判別法

一巡伝達関数が安定である場合には qu=0q_{\rm u}=0 となり、ナイキスト線図は点 (−1,j0)(-1, j0) を回転してはいけない。したがって、ナイキスト線図は点 (−1,j0)(-1, j0) を左に見ながら進まなければならない。また、ナイキスト線図の点 (−1,j0)(-1, j0) 周りの回転数を数える必要がないため、ナイキスト線図ついて ω≥0\omega\ge 0 の範囲のみ確認すれば良い。

安定余裕度

ナイキスト線図が点 (−1,j0)(-1, j0) を左に見て進むとき、一巡伝達関数が変動した際にその点を跨ぐことがないの振幅および位相の変化許容幅を安定余裕度と呼ぶ。この安定余裕度はナイキスト線図から視覚的に確認することができる。ここでは一巡伝達関数 LL が次のように記述される場合について考える。
L(s)=∏i=12ωi2s2+2ζωis+ωi2ζ=0.2ωi=(2i+1)ω0ω0=10.0\begin{align} L(s) &= \prod^{2}_{i=1}\frac{\omega_i^2}{s^2 + 2\zeta\omega_i s+ \omega_i^2} \\ \zeta &= 0.2\\ \omega_i &= (2i+1)\omega_0 \\ \omega_0 &= 10.0 \end{align}
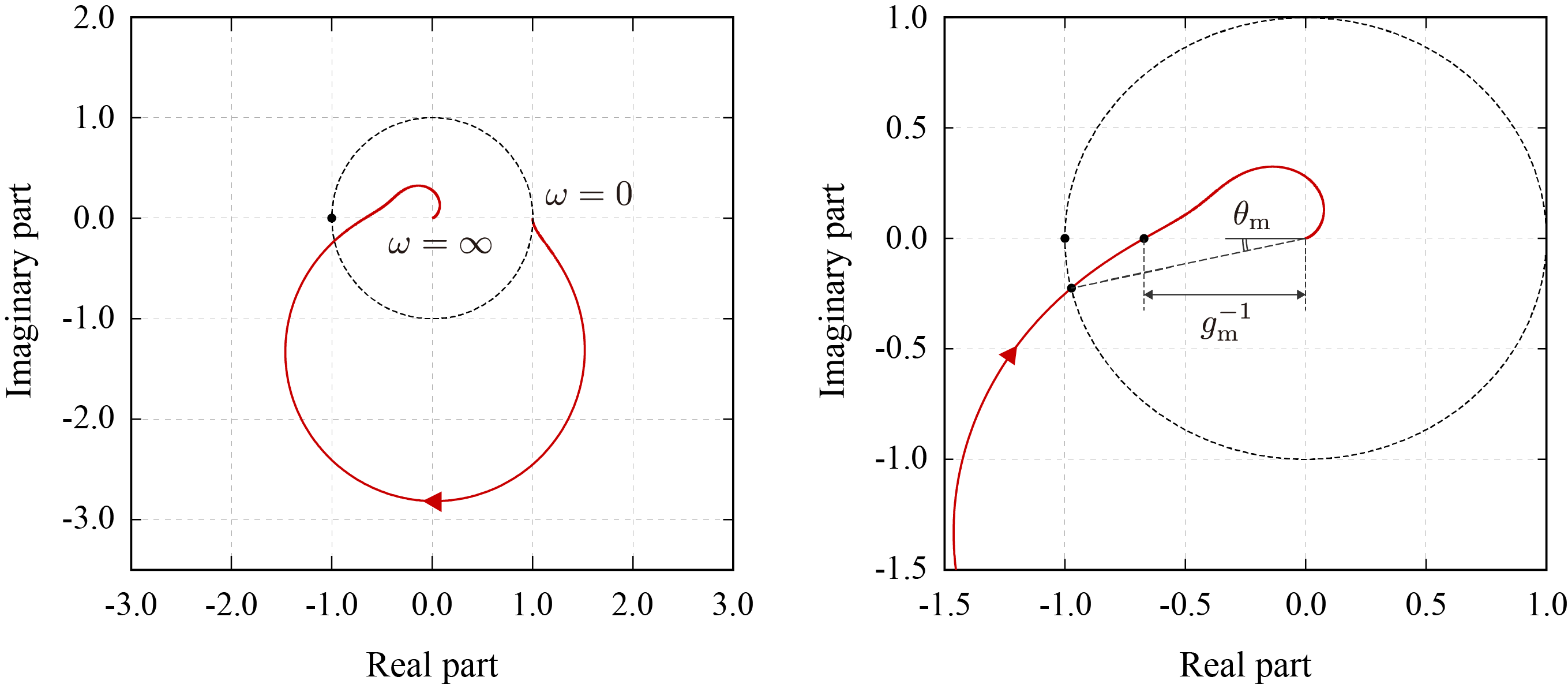
この一巡伝達関数を持つシステムのナイキスト線図は次のようになる。ただし、一巡伝達関数は不安定な極を持たないため、描画範囲を ω≥0\omega \ge 0 とした。左図は全体、右図は点 (−1,j0)(-1, j0) 近傍を表示している。
image is here
この図において gm,θmg_{\rm m}, \theta_{\rm m} がゲイン余裕、位相余裕と呼ばれる。ゲイン余裕は一巡伝達関数の位相が −π-\pi となる際の振幅の逆数となり、位相余裕は一巡伝達関数の振幅が 11 となる際の偏角となる。

特性変動耐性

システムの特性が変動した際にもシステムが安定であることをロバスト安定と呼ぶ。安定余裕度が大きければシステム変動の許容量を大きく確保することができる。以下ではゲイン変動、位相変動の影響について確認する。

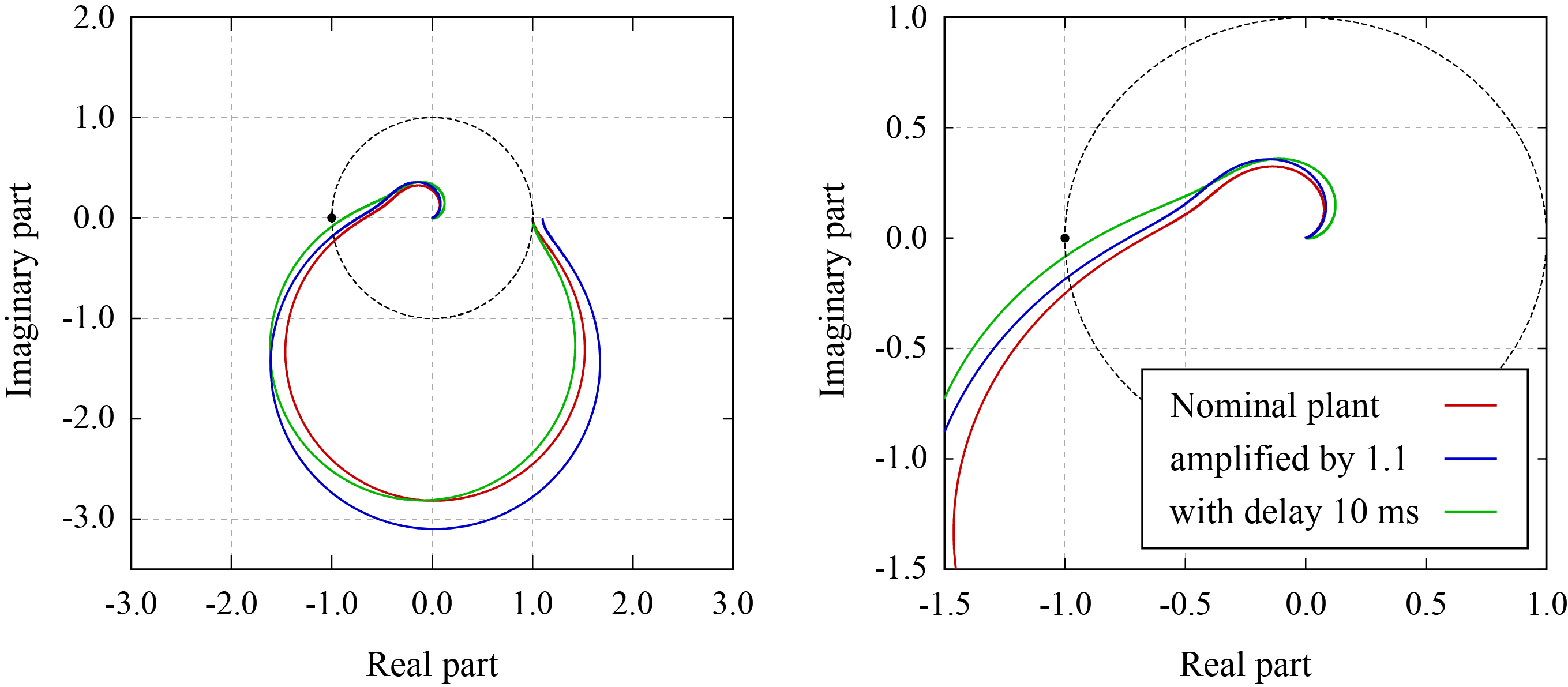
ゲイン変動について、ナイキスト線図と原点の距離はゲイン特性を表しているため、一巡伝達関数のゲインが一様に変化する場合にナイキスト線図は原点を中心として一様に拡縮する。また位相変動について、ナイキスト線図の偏角は位相特性を表すため、ナイキスト線図は位相進み要素に対して左回転し、位相遅れ要素に対して右回転する。これを確認するために、先述の一巡伝達関数に定数ゲインと時間遅れをそれぞれ付与した伝達関数を用意し、ナイキスト線図を示す。
Lg(s)=1.1L(s)Lp(s)=e−0.01sL(s)\begin{align} L_{\rm g}(s) &= 1.1L(s) \\ L_{\rm p}(s) &= e^{-0.01s}L(s) \end{align}
image is here
上図では、ゲイン増加によりナイキスト線図が膨張することで安定余裕度が減少し、また位相遅れによりナイキスト線図が左回転することで安定余裕度が減少することが確認できる。一巡伝達関数のゲイン向上は閉ループ伝達関数の周波数帯域の拡張に必要な要件であるが、位相変動はゲイン向上を阻害する要因となることに留意する必要がある。

高次システムの解析

有理関数で記述される一巡伝達関数が高次の実係数多項式を分母に持つ場合、ナイキスト線図は複素平面の実軸から見て下半平面、上半平面の両方向に向かって進む。そのため、ナイキスト線図の進む方向によって軌跡を点 (−1,j0)(-1, j0) から遠ざけるために必要な補償器の構成が異なる。ナイキスト線図の進行方向は一巡伝達関数を次のように表現することで確認することができる。
L(s)=εs2+∑i=1nκis2+2ζiωis+ωi2\begin{align} L(s) &= \frac{\varepsilon}{s^2} + \sum^{n}_{i=1} \frac{\kappa_{i}}{s^2 + 2\zeta_{i}\omega_{i}s + \omega_{i}^2} \\ \end{align}
ここで、第一項および第二項は剛体モードおよび振動モードと呼び、ε,κ\varepsilon, \kappa は剛体系としての慣性の逆数およびモード係数を表す。また、ζi,ωi\zeta_{i}, \omega_{i} は各モードの減衰率と固有角周波数を表す。このとき、正のモード係数を持つ振動モードは偏角 00 から出発して複素下半平面に向かって円を描き、負のモード係数を持つ振動モードは偏角 −π-\pi から出発して複素上半平面に向かって円を描く。これは、負のモード係数 κn\kappa_{\rm n} を持つ振動モードについて以下の式が成立するためである。
κns2+2ζωs+ω2=∣κn∣s2+2ζωs+ω2e−jπ\begin{align} \frac{\kappa_{\rm n}}{s^2 + 2\zeta\omega s + \omega^2} = \frac{|\kappa_{\rm n}|}{s^2 + 2\zeta\omega s + \omega^2}e^{-j\pi} \end{align}

三慣性共振系の例

ここでは以下に示す三慣性系を例として考える。
mx¨1=+d(x˙2−x˙1)+k(x2−x1)+fmx¨2=−d(x˙2−x˙1)−k(x2−x1)+d(x˙3−x˙2)+k(x3−x2)mx¨3=−d(x˙3−x˙2)−k(x3−x2)\begin{align} m\ddot{x}_1 &= + d(\dot{x}_2 - \dot{x}_1) + k(x_2 - x_1) + f \\ m\ddot{x}_2 &= - d(\dot{x}_2 - \dot{x}_1) - k(x_2 - x_1) + d(\dot{x}_3 - \dot{x}_2) + k(x_3 - x_2)\\ m\ddot{x}_3 &= - d(\dot{x}_3 - \dot{x}_2) - k(x_3 - x_2) \end{align}
だたし、x,f,m,d,kx, f, m, d, k はそれぞれ位置、力、慣性、粘性係数、復元力定数とする。ここで、ff から x3x_3 までの伝達関数 GG は次のように表現される。
G(s)=1ms2Z2s4+4Zs2+3Z2Z(s)≡ds+km\begin{align} G(s) &= \frac{1}{ms^2}\frac{Z^2}{s^4+4Zs^2 + 3Z^2} \\ Z(s) &\equiv \frac{ds+k}{m} \end{align}
この伝達関数を総和形式で表現する場合、以下の表現を得る。
G(s)=13ms2+−12ms2+Z+16ms2+3Z\begin{align} G(s) &= \frac{\frac{1}{3m}}{s^2} + \frac{-\frac{1}{2m}}{s^2+Z} + \frac{\frac{1}{6m}}{s^2+3Z} \end{align}
したがって、一次モードは複素上半平面に、二次モードは複素下半平面に向かって軌跡を描く。この伝達関数が一巡伝達関数となる場合のナイキスト線図を以下に示す。
image is here
剛体モードが点 (−1,j0)(-1, j0) を左に見て進み、各振動モードが点 (−1,j0)(-1, j0) から離れる条件は、剛体モードと正のモード係数を持つ振動モードに対して位相進み補償、負のモード係数を持つ振動モードに対して位相遅れ補償を当てることとなる。

CONTENTS

© DigitalServo